Comment fonctionne la calculatrice dérivée
Pour ceux qui ont une formation technique, la section suivante explique comment fonctionne la calculatrice dérivée.
Tout d’abord, un analyseur analyse la fonction mathématique. Il le transforme en une forme mieux compréhensible par un ordinateur, à savoir un arbre (voir figure ci-dessous). Ce faisant, le calculateur dérivé doit respecter l’ordre des opérations., Une spécialité dans les expressions mathématiques est que le signe de multiplication peut parfois être omis, par exemple nous écrivons « 5x » au lieu de « 5*x ». La calculatrice dérivée doit détecter ces cas et insérer le signe de multiplication.
l’analyseur est implémenté en JavaScript, basé sur L’algorithme Shunting-yard, et peut s’exécuter directement dans le navigateur. Cela permet un retour rapide lors de la saisie en transformant l’arborescence en code LaTeX. MathJax se charge de l’afficher dans le navigateur.
quand le » Go!, »le bouton est cliqué, la calculatrice dérivée envoie la fonction mathématique et les paramètres (variable de différenciation et ordre) au serveur, où elle est analysée à nouveau. Cette fois, la fonction se transforme en une forme qui peut être comprise par le système d’algèbre informatique Maxima.
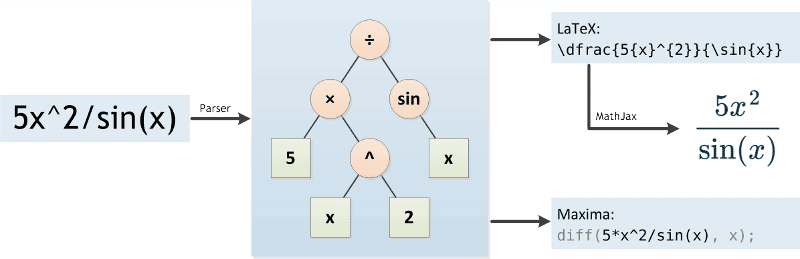
Maxima prend soin de calcul de la dérivée de la fonction mathématique. Comme tout système d’algèbre informatique, il applique un certain nombre de règles pour simplifier la fonction et calculer les dérivées selon les règles de différenciation communément connues., La sortie de Maxima est à nouveau transformée en LaTeX et est ensuite présentée à l’utilisateur.
L’affichage des étapes de calcul est un peu plus impliqué, car le calculateur dérivé ne peut pas complètement dépendre de Maxima pour cette tâche. Au lieu de cela, les dérivés doivent être calculés manuellement étape par étape. Les règles de différenciation (Règle du produit, Règle du quotient, règle de la chaîne, rule) ont été implémentées en code JavaScript. Il existe également un tableau des fonctions dérivées pour les fonctions trigonométriques et la racine carrée, le logarithme et la fonction exponentielle., Dans chaque étape de calcul, une opération de différenciation est effectuée ou réécrit. Par exemple, les facteurs constants sont retirés des opérations de différenciation et les sommes sont divisées (règle de la somme). Ceci, et les simplifications générales, est fait par Maxima. Pour chaque dérivée calculée, les représentations LaTeX des expressions mathématiques résultantes sont marquées dans le code HTML afin que la surbrillance soit possible.
la fonction « Vérifier la réponse » doit résoudre la tâche difficile de déterminer si deux expressions mathématiques sont équivalentes., Leur différence est calculée et simplifiée autant que possible en utilisant Maxima. Par exemple, cela implique d’écrire des fonctions trigonométriques/hyperboliques sous leurs formes exponentielles. S’il peut être montré que la différence se simplifie à zéro, la tâche est résolue. Sinon, un algorithme probabiliste est appliqué qui évalue et compare les deux fonctions à des endroits choisis au hasard.
les graphiques de fonctions interactives sont calculés dans le navigateur et affichés dans un élément canvas (HTML5)., Pour chaque fonction à représenter graphiquement, la calculatrice crée une fonction JavaScript, qui est ensuite évaluée par petites étapes afin de dessiner le graphique. Lors de la représentation graphique, les singularités (par exemple les pôles) sont détectées et traitées spécialement. Le contrôle gestuel est implémenté à L’aide de Hammer.js.
Si vous avez des questions ou des idées pour améliorer la calculatrice dérivée, n’hésitez pas à m’écrire un e-mail.
