la façon la plus simple de saisir l’idée d’une population croissante est avec un organisme unicellulaire, tel qu’une bactérie ou un cilliate. Dans la Figure 1, une population de Paramecium dans une petite diapositive de dépression de laboratoire est illustrée. Dans cette population, les individus se divisent une fois par jour. Ainsi, en commençant par un seul individu au jour 0, nous attendons, en jours successifs, 2, 4, 8, 16, 32, et 64 individus dans la population., Nous pouvons voir ici que, un jour donné, le nombre d’individus dans la population est simplement le double de ce que le nombre était la veille, donc le nombre aujourd’hui, appelez-le N(aujourd’hui), est égal au double du nombre d’hier, appelez-le N(hier), que nous pouvons écrire de manière plus compacte comme N(aujourd’hui) = 2n(hier).
Il est donc logique d’écrire ceci comme, N(t) = 2n(t – 1) Où t pourrait prendre n’importe quelle valeur.,
Maintenant, nous pouvons généraliser cette idée un peu si l’on remarque qu’au jour six le nombre est égal à deux fois le nombre à cinq jours, ou N(6) = 2N(5) et au jour cinq le nombre est égal à deux fois le nombre à quatre jours, ou N(5) = 2N(4), etc.
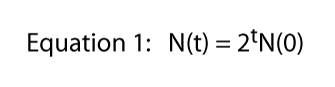
où t représente le temps (par exemple, si t = 6, N(6) = 26).
enfin, nous notons que cette équation a été dérivée de la situation spécifique illustrée à la Figure 1, où une division par jour était la règle dure et rapide., C’est de là que vient le 2 dans L’équation 1 — de chaque paramécium individuel, nous obtenons deux individus le lendemain. Bien sûr, le taux de division pourrait être n’importe quoi. S’il y avait deux divisions par jour mais qu’une cellule mourait toujours, nous nous attendrions à trois individus de chaque individu et L’équation 1 serait N(t) = 3tN(0)., Ainsi, le taux de division pourrait être n’importe quel nombre et l’équation générale devient,
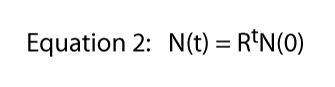
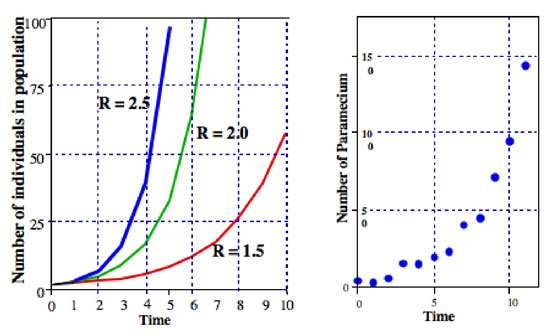
où R est généralement appelé le taux fini d’augmentation de la population (dans le cas réel de la division le taux fini d’augmentation de la population est égal au taux de division). La Figure 2 illustre cette équation pour différentes valeurs de R. Il est normalement appelé l’équation exponentielle, et la forme de données dans la Figure 2 représente la forme générale appelée exponentielle.,
n’Importe quelle valeur de R peut être représenté par un nombre infini de façons (par exemple, si R = 16, on peut écrire R = 8 x 2, ou R = 42, ou R = 32/2, ou R = 2.718282.77). Cette dernière expression (R = 2.718282.,77) utilise une constante importante qui pourrait être rappelée du calcul élémentaire, la constante d’Euler. Exprimer n’importe quelle valeur de R en tant que constante d’Euler élevée à une certaine puissance est en fait extrêmement utile — il apporte toute la puissance du calcul dans l’image.,olize la constante d’Euler e, nous pouvons écrire l’Équation 2
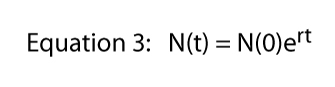
Maintenant, si nous prenons le logarithme naturel des deux côtés de l’Équation 3 — rappelez-vous, ln(ex) = x — Équation 3 devient: ln = ln + rt
Et si nous avons commencé la population avec un seul individu (comme dans l’exemple ci-dessus), nous avons

à partir de laquelle nous voyons que le logarithme naturel de la population, à un moment donné, est une constante, temps que temps., La constante r est appelée le taux intrinsèque d’augmentation naturelle (Figure 2).
toutes sortes de micro-organismes présentent des profils très proches de la croissance exponentielle de la population. Par exemple, dans le graphique de droite de la Figure 2 est une population de Paramecium croissant dans une culture de laboratoire. Le modèle de croissance est très proche du modèle de l’équation exponentielle.
Une autre façon d’écrire l’équation exponentielle est une équation différentielle, c’est-à-dire représentant la croissance de la population sous sa forme dynamique., Plutôt que de demander Quelle est la taille de la population à l’instant t, nous demandons quel est le taux de croissance de la population à l’instant T. le taux est symbolisé par dN/dt, ce qui signifie simplement « changement de N par rapport au changement de t”, et si vous vous souvenez de votre calcul de base, nous pouvons trouver le taux de croissance en différenciant L’équation 4, ce qui nous donne
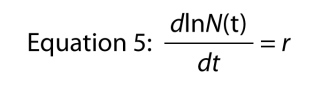
Ce Qui est assez remarquable, car il dit que le taux de croissance du log du nombre dans la population est constant. , Ce taux constant de croissance du logarithme de la population est le taux intrinsèque d’augmentation.,
Rappelons que le taux de changement du journal d’un nombre est le même que le « per capita” le changement de nombre, ce qui signifie que nous pouvons écrire l’Équation (5) comme

où nous omettons la variable t, car il est évident où il va, et puis nous réorganiser un peu à venir avec
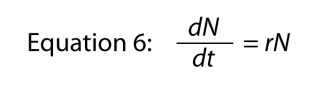
où le paramètre r est, encore une fois, le taux intrinsèque d’accroissement naturel., La relation de base entre le taux fini d’augmentation et le taux intrinsèque est
r = Ln(R)
où ln fait référence au logarithme naturel. Noter que l’Équation (6) et l’Équation 3 sont juste différentes formes de la même équation (Équation 3 est la forme intégrée de l’Équation (6); l’Équation (6) est la forme différenciée de l’Équation (3), et les deux peuvent être appelés simplement l’équation exponentielle.,

L’équation exponentielle est un modèle utile de simple populations, au moins pour un temps relativement court., Par exemple, si un technicien de laboratoire a besoin de savoir quand une culture bactérienne atteint une certaine densité de population, l’équation exponentielle peut être utilisée pour fournir une prédiction quant au moment exact où cette taille de population sera atteinte. Un autre exemple est dans le cas des ravageurs agricoles. Les Herbivores sont toujours potentiellement des problèmes majeurs pour les plantes. Lorsque les plantes soumises à de telles épidémies sont agricoles, c’est-à-dire des cultures, la perte peut être très importante pour l’agriculteur et le consommateur. Ainsi, il y a toujours une pression pour prévenir de telles épidémies., Depuis la Seconde Guerre mondiale, les pesticides chimiques, tels que le DDT, constituent la principale arme de lutte contre ces épidémies. Cependant, ces dernières années, nous nous sommes rendu compte que ces pesticides sont extrêmement dangereux à long terme, à la fois pour l’environnement et pour les personnes. Par conséquent, il y a eu un mouvement pour limiter la quantité de pesticides pulvérisés pour lutter contre les ravageurs. La principale façon de le faire est d’établir un seuil économique, qui est la densité de population du ravageur potentiel en dessous de laquelle les dommages à la culture sont insignifiants (c’est-à-dire qu’il n’est pas vraiment nécessaire de pulvériser)., Lorsque la population de ravageurs dépasse ce seuil, l’agriculteur doit prendre des mesures et appliquer une sorte de pesticide ou d’autres moyens de lutter contre le Ravageur. Compte tenu de la nature de ce problème, il est parfois de la plus haute importance de pouvoir prédire quand le Ravageur atteindra le seuil économique. Connaître le R pour l’espèce nuisible permet à l’agriculteur de prédire quand il sera nécessaire d’appliquer une sorte de procédure de contrôle (Figure 3).
L’équation exponentielle est également un modèle utile pour développer des idées intuitives sur les populations., L’exemple classique est un étang avec une population de nénuphars. Si chaque Nénuphar se reproduit (deux nénuphars remplacent l’un d’eux) chaque mois, et qu’il a fallu, disons, trois ans pour que l’étang soit à moitié rempli de nénuphars, combien de temps faudra-t-il pour que l’étang soit complètement recouvert de nénuphars? Si vous ne vous arrêtez pas pour penser trop clairement, il est tentant de dire qu’il faudra autant de temps, trois ans, pour que la seconde moitié de l’étang soit aussi remplie que la première. La réponse, bien sûr, est d’un mois.,
un autre exemple populaire est l’Ancien mathématicien égyptien proverbial (ou parfois persan) qui demande le paiement du roi sous forme de grains de blé (parfois de riz). Un grain sur la première case d’un échiquier, deux grains sur la deuxième case, et ainsi de suite, jusqu’à la dernière case. Le Pharaon ne peut pas imaginer qu’un paiement aussi simple pourrait représenter beaucoup, et est donc d’accord. Mais il n’a pas pleinement apprécié la croissance exponentielle., Comme il y a 64 cases sur l’échiquier, nous pouvons utiliser L’équation 2 pour déterminer combien de grains de blé devront payer sur le dernier carré (R élevé à la 64e puissance, soit environ 18 446 744 074 000 000 000 — beaucoup de blé en effet, certainement plus que dans tout le Royaume). Ces exemples soulignent la façon souvent surprenante dont un processus exponentiel peut conduire à de très grands nombres très rapidement.
