Réponse Rapide:
Pour un triangle rectangle:

La fonction sinus sin prend de l’angle θ et donne le rapport à l’opposé hypoténuse
l’inverse de La fonction sinus sin-1 prend le ratio oppositehypotenuse et donne l’angle θ
Et du cosinus et de la tangente de suivre une idée similaire.,
Et maintenant pour les détails:
Sinus, Cosinus et Tangente sont tous basés sur un Triangle rectangle
Ils sont très des fonctions similaires … nous allons donc regarder la fonction sinus, puis le sinus Inverse pour apprendre de quoi il s’agit.,
la Fonction Sinus
Le Sinus de l’angle θ est:
- la longueur du côté Opposé à l’angle θ
- divisé par la longueur de l’Hypoténuse
Ou plus simplement:
sin(θ) = Opposé / Hypoténuse
La Fonction Sinus peuvent nous aider à résoudre ce genre de choses:
Fonction Sinus Inverse
Mais parfois, c’est l’angle que nous devons trouver.
c’est là que « sinus Inverse » entre en jeu.
Il répond à la question » quel angle a sinus égal à opposé / hypoténuse?, »
le symbole du sinus inverse est sin-1, ou parfois arcsin.
ils sont comme en avant et en arrière!

- sin prend un angle et nous donne le ratio « opposé/hypoténuse »
- sin-1 prend le ratio « opposé/hypoténuse » et nous donne l’angle.
Exemple:
Calculatrice
 |
Sur la calculatrice, vous appuyez sur l’une des suivantes (selon votre marque de calculatrice):soit « 2ndF péché » ou » maj « (shift péché ». |
Sur votre calculatrice, essayez d’utiliser le péché et puis sin-1 pour voir ce qui se passe
Plus d’Un Angle!
le sinus Inverse ne vous montre qu’un angle … mais il y a plus d’angles qui pourrait fonctionner.
Exemple: Voici deux angles où opposé/hypoténuse = 0.,5
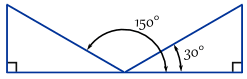
en fait, il y a infiniment d’angles, parce que vous pouvez continuer à ajouter (ou soustraire) 360°:
rappelez-vous ceci, car il y a des moments où vous avez réellement besoin d’un des autres angles!
Résumé
Le Sinus de l’angle θ est:
sin(θ) = Opposé / Hypoténuse
Et Sinus Inverse est :
sin-1 (à l’Opposé / Hypoténuse) = θ
Qu’ « cos » et « tan » … ?
exactement la même idée, mais des rapports latéraux différents.,
Cosinus
Le Cosinus de l’angle θ est:
cos(θ) = Adjacent / Hypoténuse
Et Cosinus Inverse est :
cos-1 (Adjacent / Hypoténuse) = θ
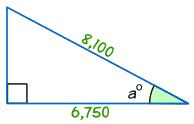
Exemple: Trouver la taille de l’angle a°
cos a° = Adjacent / Hypoténuse
cos a° = 6,750/de 8 100 = 0.8333…
a° = cos-1 (0,8333…) = 33.,6° (à la 1re décimale)
Tangente
La Tangente de l’angle θ est:
tan(θ) = Opposé / Adjacent
Donc l’Inverse de la Tangente est :
tan-1 (à l’Opposé / Adjacent) = θ
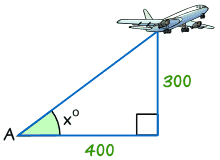
Exemple: Trouver la taille de l’angle x°
tan x° = Opposé / Adjacent
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (bon à la 1re décimale)
les Autres Noms
Parfois, sin-1 est appelé asin ou arcsin
de Même, cos-1 est appelé acos ou arccos
Et tan-1 est appelé atan ou arctan
Exemples:
- arcsin(y) est la même que sin-1(y)
- atan(θ) est la même que tan-1(θ)
- etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- Mais le sinus Inverse et le cosinus Inverse ne « vont pas éternellement » comme le sinus et le cosinus …
regardons l’exemple du cosinus.
Voici le cosinus et le cosinus Inverse tracés sur le même graphique:
cosinus et cosinus Inverse
Ce sont des images miroir (à propos de la diagonale)
Mais pourquoi le cosinus Inverse est-il coupé en haut et en bas (les points ne font pas vraiment partie de la fonction) … ?
Parce que pour être une fonction qu’il ne peut donner qu’une seule réponse
lorsque nous demandons « qu’est-ce que cos-1(x) ?, »
une réponse ou infiniment de réponses
Mais nous avons vu plus tôt qu’il y a infiniment de réponses, et la ligne pointillée sur le graphique le montre.
alors oui, il y a une infinité de réponses …
… mais imaginez que vous tapez 0.5 dans votre calculatrice, appuyez sur cos – 1 et il vous donne une liste sans fin de réponses possibles …
nous avons Donc cette règle qu’une fonction ne peut donner qu’une seule réponse.
donc, en le coupant comme ça, nous obtenons une seule réponse, mais nous devrions nous rappeler qu’il pourrait y avoir d’autres réponses.,
la Tangente et arctangente
Et voici la fonction tangente et arctangente. Pouvez-vous voir comment ils sont des images miroir (sur la diagonale) …?

Tangente

Tangente Inverse



