Après la construction d’une machine modèle d’apprentissage, la prochaine étape consiste à évaluer la performance du modèle et de comprendre comment notre modèle est à l’encontre d’un modèle de référence., La mesure d’évaluation à utiliser dépend du type de problème que vous essayez de résoudre —qu’il s’agisse d’un problème supervisé ou non supervisé, et s’il s’agit d’une tâche de classification ou de régression.
dans cet article, je vais parler de deux mesures d’évaluation importantes utilisées pour les problèmes de régression et mettre en évidence la différence clé entre elles.
Le R-carré, également connu sous le nom de détermination du coefficient, définit le degré auquel la variance de la variable dépendante (ou cible) peut être expliquée par la variable indépendante (Caractéristiques).,
comprenons cela avec un exemple — disons que la valeur R au carré pour un modèle particulier est 0.7. Cela signifie que 70% de la variation de la variable dépendante est expliquée par les variables indépendantes.
idéalement, Nous voudrions que les variables indépendantes soient capables d’expliquer toute la variation de la variable cible. Dans ce scénario, la valeur r au carré serait 1. On peut donc dire que plus la valeur r carré, mieux dans le modèle.,
donc, en termes simples, plus le r au carré est élevé, plus la variation est expliquée par vos variables d’entrée et donc meilleur est votre modèle. En outre, le r-carré serait compris entre 0 et 1. Voici la formule pour calculer R-squared –
Le R-squared est calculé en divisant la somme des carrés des résidus du modèle de régression (donné par SSres) par la somme totale des carrés des erreurs du modèle moyen (donné par SStot), puis en le soustrayant de 1.,
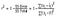
Un inconvénient de r-au carré est qu’il suppose que toutes les variables contribue à expliquer la variation de la cible, ce qui pourrait ne pas être toujours le cas. Par exemple, si nous ajoutons de nouvelles fonctionnalités aux données (qui peuvent être utiles ou non), la valeur r au carré pour le modèle augmenterait ou resterait la même mais elle ne diminuerait jamais.
Ceci est pris en charge par une version légèrement modifiée de r-squared, appelée R-squared ajusté.,
R-carré ajusté
semblable à R-carré, le R-carré ajusté mesure la variation de la variable dépendante (ou cible), expliquée uniquement par les caractéristiques qui sont utiles pour faire des prédictions. Contrairement à R-squared, le R-squared ajusté vous pénaliserait pour l’ajout de fonctionnalités qui ne sont pas utiles pour prédire la cible.
comprenons mathématiquement comment cette caractéristique est logée dans le R-carré ajusté., Voici la formule pour adjusted r-squared

Ici, R^2 est le r-carré calculé, N est le nombre de lignes et M est le nombre de colonnes. À mesure que le nombre d’entités augmente, la valeur du dénominateur diminue.
- Si le R2 augmente d’une valeur significative, alors le r carré ajusté augmenterait.
- S’il n’y a pas de changement significatif dans R2, alors le R2 ajusté diminuerait.
