Statistiques 2 – Coefficient de Corrélation et le Coefficient de Détermination

la quantité r, appelée coefficient de corrélation linéaire, mesure la force et
la direction d’une relation linéaire entre deux variables. Le coefficient de corrélation linéaire
est parfois appelé coefficient de corrélation de moment de produit de Pearson en
honneur de son développeur Karl Pearson.
La formule mathématique pour computingr est: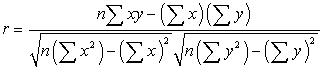

où n est le nombre de paires de données.,
(N’Êtes-vous pas content d’avoir une calculatrice graphique qui calcule cette formule?)
La valeur de r est telle que -1 < r < +1. Les signes + et – sont utilisés pour les corrélations linéaires positives
et les corrélations linéaires négatives, respectivement.
corrélation Positive: Si x et y ont une forte corrélation linéaire positive,r est proche
à +1. Une valeur r De exactement + 1 indique un ajustement positif Parfait., Les valeurs positives
indiquent une relation entre les variables x et y telle que lorsque les valeurs pour x augmentent,
Les valeurs pour y augmentent également.
corrélation négative: si x et y ont une forte corrélation linéaire négative,r est proche
de -1. Une valeur r De exactement -1 indique un ajustement négatif parfait. Les valeurs négatives
indiquent une relation entre x et y telle que lorsque les valeurs pour x augmentent, les valeurs
pour y diminuent.
Aucune corrélation: Si il n’y a pas de corrélation linéaire ou une faible corrélation linéaire, r
proche de 0., Une valeur proche de zéro signifie qu’il existe une relation aléatoire et non linéaire
entre les deux variables
notez que r est une quantité sans dimension; c’est-à-dire qu’elle ne dépend pas des unités
employées.
une corrélation parfaite de ± 1 ne se produit que lorsque les points de données se trouvent tous exactement sur une
ligne droite. Si r = +1, la pente de cette droite est positif. Si r = -1, la pente de cette ligne
est négative.
Une corrélation supérieure à 0,8 est généralement décrite comme forte, alors qu’une corrélation
à moins de 0.,5 est généralement décrit commefaible. Ces valeurs peuvent varier en fonction du
« type » de données examinées. Une étude utilisant des données scientifiques peut nécessiter une corrélation
plus forte qu’une étude utilisant des données de sciences sociales.

Le coefficient de détermination r 2,est utile car elle donne la proportion de
la variance (fluctuation) d’une variable qui est prévisible à partir de l’autre variable.,
c’est une mesure qui nous permet de déterminer à quel point on peut être certain de faire des
prédictions à partir d’un certain modèle/graphique.
le coefficient de détermination est le rapport de la variation expliquée à la variation totale
.
Le coefficient de détermination est telle que 0 < r 2 < 1, et indique la force
de l’association linéaire entre x et y.,
Le coefficient de détermination représente le pourcentage de données qui est le plus proche
à la ligne de meilleur ajustement. Par exemple, si r = 0,922, alors r 2 = 0,850, ce qui signifie que
85% de la variation totale iny peut être expliqué par la relation linéaire entre x
et y (comme décrit par l’équation de régression). Les 15% restants de la variation totale
en y restent inexpliqués.
Le coefficient de détermination est une mesure de la façon dont la ligne de régression
représente les données., Si la droite de régression passe exactement par chaque point du nuage de points
, elle serait en mesure d’expliquer toute la variation. Plus la ligne est éloignée des points, moins elle est capable d’expliquer.