
Dans cet article, vous apprendrez tout sur les SVM ou Machine à Vecteurs de Support, qui est l’un des plus populaires des algorithmes d’IA (c’est l’un des top 10 des algorithmes d’IA) et sur le Noyau Truc, qui traite de la non-linéarité et de dimensions supérieures., Nous aborderons des sujets comme les hyperplans, les multiplicateurs de Lagrange, nous aurons des exemples visuels et des exemples de code (similaires à l’exemple de code utilisé dans le chapitre KNN) pour mieux comprendre cet algorithme très important.
SVM Explained
La Machine à Vecteurs de Support est un algorithme d’apprentissage supervisé principalement utilisé pour la classification mais il peut également être utilisé pour la régression. L’idée principale est que sur la base des données étiquetées (données d’entraînement) l’algorithme essaie de trouver le meilleur hyperplane qui peut être utilisé pour classer de nouveaux points de données. En deux dimensions, l’hyperplan est une ligne simple.,
habituellement, un algorithme d’apprentissage essaie d’apprendre les caractéristiques les plus courantes (ce qui différencie une classe d’une autre) d’une classe et la classification est basée sur ces caractéristiques représentatives apprises (donc la classification est basée sur les différences entre les classes). Le SVM fonctionne dans l’autre sens. Il trouve les exemples les plus similaires entre les classes. Ce seront les vecteurs de support.
Comme exemple, considérons deux classes, les pommes et les citrons.,
D’autres algorithmes apprendront les caractéristiques les plus évidentes et les plus représentatives des pommes et des citrons, comme les pommes sont vertes et arrondies tandis que les citrons sont jaunes et ont une forme elliptique.
en revanche, SVM recherchera des pommes qui sont très similaires aux citrons, par exemple des pommes qui sont jaunes et ont une forme elliptique. Ce sera un vecteur de support. L’autre vecteur de support sera un citron semblable à une pomme (vert et arrondi). Ainsi, d’autres algorithmes apprennent les différences tandis que SVM apprend les similitudes.,
Si nous visualisons l’exemple ci-dessus en 2D, nous aurons quelque chose comme ceci:

Comme nous aller de gauche à droite, tous les exemples seront classés comme des pommes jusqu’à ce que nous arrivons à la pomme jaune. À partir de ce moment, la confiance qu’un nouvel exemple est une pomme diminue tandis que la confiance de la classe citron augmente., Lorsque la confiance de la classe citron devient supérieure à la confiance de la classe pomme, les nouveaux exemples seront classés comme citrons (quelque part entre la pomme jaune et le citron vert).
sur la base de ces vecteurs de support, l’algorithme essaie de trouver le meilleur hyperplan qui sépare les classes. En 2D, le hyperplane est d’une ligne, donc il devrait ressembler à ceci:

Ok, mais pourquoi ai-je tirer le bleu de la frontière comme dans l’image ci-dessus?, J’ai également pu tracer les frontières comme ceci:

Comme vous pouvez le voir, nous avons un nombre infini de possibilités de tirer la décision de la frontière. Alors, comment pouvons-nous trouver le meilleur?
trouver L’hyperplan Optimal
intuitivement, la meilleure ligne est la ligne qui est loin des exemples apple et lemon (a la plus grande marge)., Pour avoir une solution optimale, nous devons maximiser la marge dans les deux sens (si nous avons plusieurs classes, alors nous avons l’optimiser en considérant chacune des classes).

Donc, si l’on compare la photo ci-dessus avec l’image ci-dessous, nous pouvons facilement observer, que la première qui est optimal hyperplane (en ligne) et la deuxième est une sous-solution optimale, car la marge est beaucoup plus courte.,

Parce que nous voulons maximiser les marges de prendre en considération toutes les classes, au lieu d’utiliser une marge pour chaque classe, nous utilisons un « global” de la marge, qui prend en considération toutes les classes., Cette marge de ressembler à la ligne violette dans l’image suivante:

Cette marge est orthogonal à la frontière et à égale distance entre les vecteurs de soutien.
alors, où avons-nous des vecteurs? Chacun des calculs (calculer la distance et les hyperplans optimaux) sont effectués dans l’espace vectoriel, de sorte que chaque point de données est considéré comme un vecteur. La dimension de l’espace est définie par le nombre d’attributs des exemples., Pour comprendre les mathématiques derrière, veuillez lire cette brève description mathématique des vecteurs, des hyperplans et des optimisations: SVM Succintly.
dans l’ensemble, les vecteurs de support sont des points de données qui définissent la position et la marge de l’hyperplan. Nous les appelons vecteurs « support », car ce sont les points de données représentatifs des classes, si nous déplaçons l’un d’entre eux, la position et/ou la marge changeront. Le déplacement d’autres points de données n’aura pas d’effet sur la marge ou la position de l’hyperplan.,
pour faire des classifications, nous n’avons pas besoin de tous les points de données d’entraînement (comme dans le cas de KNN), nous devons enregistrer uniquement les vecteurs de support. Dans le pire des cas, tous les points seront des vecteurs de support, mais cela est très rare et si cela se produit, vous devriez vérifier votre modèle pour les erreurs ou les bogues.
donc, fondamentalement, l’apprentissage équivaut à trouver l’hyperplan avec la meilleure marge, c’est donc un simple problème d’optimisation.,/h2>
Les étapes de base de la SVM sont les suivantes:
- sélectionner deux hyperplans (en 2D) qui séparent les données sans points entre eux (lignes rouges)
- maximiser leur distance (la marge)
- la ligne moyenne (ici la ligne à mi-chemin entre les deux lignes rouges) sera la limite de décision
c’est très agréable et facile, mais trouver la meilleure marge, le problème d’optimisation n’est pas trivial (c’est facile 2D, quand nous n’avons que deux attributs, mais que faire si nous avons N dimensions avec n un très grand nombre)
pour résoudre le problème d’optimisation, nous utilisons les multiplicateurs de Lagrange., Pour comprendre cette technique, vous pouvez lire les deux articles suivants: dualité multiplicateur de Langrange et une explication Simple de pourquoi les multiplicateurs de Langrange Wroks.
Jusqu’à présent, nous avions des données linéairement séparables, nous pouvions donc utiliser une ligne comme limite de classe. Mais que faire si nous devons faire face à des ensembles de données non linéaires?,
SVM Non Linéaire des Ensembles de Données
Un exemple de la non linéaire des données est:

Dans ce cas, nous ne pouvons pas trouver une ligne droite pour séparer les pommes de citrons. Alors, comment pouvons-nous résoudre ce problème. Nous allons utiliser L’Astuce du noyau!
l’idée de base est que lorsqu’un ensemble de données est inséparable dans les dimensions actuelles, ajoutez une autre dimension, peut-être que de cette façon les données seront séparables., Pensez-y, l’exemple ci-dessus est en 2D et il est inséparable, mais peut-être qu’en 3D il y a un écart entre les pommes et les citrons, peut-être qu’il y a une différence de niveau, donc les citrons sont au niveau un et les citrons sont au niveau deux. Dans ce cas, nous pouvons facilement dessiner un hyperplan de séparation (en 3D, un hyperplan est un plan) entre les niveaux 1 et 2.
mappage à des Dimensions supérieures
Pour résoudre ce problème, nous ne devrions pas simplement ajouter aveuglément une autre dimension, nous devrions transformer l’espace afin de générer cette différence de niveau intentionnellement.,
mappage de la 2D à la 3D
supposons que nous ajoutions une autre dimension appelée X3. Une autre transformation importante est que dans la nouvelle dimension, les points sont organisés en utilisant cette formule x12 + x22.
Si nous avons tracé le plan défini par le x2 + y2 formule, nous allons obtenir quelque chose comme ceci:

Maintenant, nous avons à la carte les pommes et les citrons (qui sont de simples points) pour ce nouvel espace. Pensez-y bien, qu’avons-nous fait?, Nous venons d’utiliser une transformation dans laquelle nous avons ajouté des niveaux basés sur la distance. Si vous êtes à l’origine, les points seront au plus bas niveau. Lorsque nous nous éloignons de l’origine, cela signifie que nous montons la colline (en nous déplaçant du centre du plan vers les marges), de sorte que le niveau des points sera plus élevé., Maintenant si l’on considère que l’origine est le citron du centre, nous aurons quelque chose comme ceci:
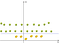
Maintenant, on peut facilement séparer les deux classes. Ces transformations sont appelées noyaux. Les noyaux populaires sont: noyau Polynomial, noyau gaussien, fonction de base radiale (RBF), noyau Laplace RBF, noyau sigmoïde, noyau Anove RBF, etc. (voir fonctions du noyau ou une description plus détaillée des noyaux D’apprentissage automatique).,
la Cartographie de 1D 2D
un Autre, exemple facile en 2D serait:

Après en utilisant le noyau et après toutes les transformations que nous allons obtenir:

Donc, après la transformation, nous pouvons facilement délimiter les deux classes à l’aide d’une seule ligne.,
dans les applications réelles, nous n’aurons pas une simple ligne droite, mais nous aurons beaucoup de courbes et de dimensions élevées. Dans certains cas, nous n’aurons pas deux hyperplans qui séparent les données sans points entre eux, nous avons donc besoin de compromis, de tolérance pour les valeurs aberrantes. Heureusement, L’algorithme SVM a un paramètre dit de régularisation pour configurer le compromis et tolérer les valeurs aberrantes.
réglage des paramètres
Comme nous l’avons vu dans la section précédente, choisir le bon noyau est crucial, car si la transformation est incorrecte, le modèle peut avoir de très mauvais résultats., En règle générale, Vérifiez toujours si vous avez des données linéaires et dans ce cas, utilisez toujours un SVM linéaire (noyau linéaire). Le SVM linéaire est un modèle paramétrique, mais pas un SVM du noyau RBF, donc la complexité de ce dernier augmente avec la taille de l’ensemble d’apprentissage. Non seulement il est plus coûteux de former une SVM du noyau RBF, mais vous devez également garder la matrice du noyau, et la projection dans cet espace de dimension supérieure « infinie” où les données deviennent linéairement séparables est également plus chère pendant la prédiction., De plus, vous avez plus d’hyperparamètres à régler, donc la sélection du modèle est également plus chère! Et enfin, il est beaucoup plus facile de surajuster un modèle complexe!
régularisation
le paramètre régularisation (en python, il s’appelle C) indique à L’optimisation SVM combien vous voulez éviter de manquer de classer chaque exemple de formation.
Si le C est plus élevé, l’optimisation choisira un hyperplan à marge plus petite, de sorte que le taux de classification des données d’entraînement sera inférieur.,
d’autre part, si le C est faible, alors la marge sera grande, même s’il y aura des exemples de données d’entraînement classées manquantes. Ceci est illustré dans les deux diagrammes:

Comme vous pouvez le voir dans l’image, lorsque le C est faible, la marge est plus élevée (donc implicitement nous n’avons pas tellement le nombre de courbes, la ligne n’est pas strictement suit les points de données), même si deux pommes ont été classés comme des citrons., Lorsque le C est élevé, la limite est pleine de courbes et toutes les données d’entraînement ont été classées correctement. N’oubliez pas, même si toutes les données d’entraînement ont été correctement classées, cela ne signifie pas que l’augmentation du C augmentera toujours la précision (en raison d’un surajustement).
Gamma
Le prochain paramètre important est le Gamma. Le paramètre gamma définit jusqu’où l’influence d’un seul exemple d’entraînement atteint. Cela signifie que High Gamma ne considérera que les points proches de l’hyperplan plausible et low Gamma considérera les points à plus grande distance.,

comme vous pouvez le voir, la diminution du gamma entraînera la recherche de l’hyperplan correct considérera les points à de plus grandes distances, de sorte que de plus en plus de points seront utilisés (les lignes vertes indiquent quels points ont été pris en compte lors de la recherche de l’hyperplan optimal).
Margin
le dernier paramètre est La marge. Nous avons déjà parlé de marge, de marge plus élevée, de meilleur modèle, donc de meilleure classification (ou prédiction)., La marge doit toujours être maximisée.
exemple SVM utilisant Python
dans cet exemple, nous allons utiliser le Social_Networks_Ads.fichier csv, le même fichier que nous avons utilisé dans l’article précédent, voir Exemple KNN en utilisant Python.
dans cet exemple, Je ne noterai que les différences entre SVM et KNN, car je ne veux pas me répéter dans chaque article! Si vous voulez toute l’explication sur la façon dont nous pouvons lire l’ensemble de données, comment analyser et diviser nos données ou comment pouvons-nous évaluer ou tracer les limites de décision, veuillez lire l’exemple de code du chapitre précédent (KNN)!,
parce que la bibliothèque sklearn est une bibliothèque Python très bien écrite et utile, nous n’avons pas trop de code à changer. La seule différence est que nous devons importer la classe SVC (SVC = SVM dans sklearn) à partir de sklearn.svm au lieu de la classe KNeighborsClassifier de sklearn.voisin.
Après avoir importé Le SVC, nous pouvons créer notre nouveau modèle en utilisant le constructeur prédéfini. Ce constructeur a de nombreux paramètres, mais je ne décrirai que les plus importants, la plupart du temps vous n’utiliserez pas d’autres paramètres.,
les paramètres Les plus importants sont:
- noyau: le noyau de type à être utilisé. Les noyaux les plus courants sont rbf (c’est la valeur par défaut), poly ou sigmoid, mais vous pouvez également créer votre propre noyau.,
- C: c’est le paramètre de régularisation décrit dans la section Paramètres de réglage
- gamma: cela a également été décrit dans la section Paramètres de réglage
- degré: il n’est utilisé que si le noyau choisi est poly et définit le degré du polinom
- probabilité: c’est un paramètre booléen et si c’est vrai, alors le modèle retournera pour chaque prédiction, le vecteur de probabilités d’appartenir à chaque classe de la variable de réponse. Donc, fondamentalement, il vous donnera les confidences pour chaque prédiction.,
- shrinking: cela montre si vous voulez ou non qu’une heuristique shrinking soit utilisée dans votre optimisation de la SVM, qui est utilisée dans L’optimisation minimale séquentielle. Sa valeur par défaut est true, et si vous n’avez pas de bonne raison, veuillez ne pas changer cette valeur en false, car le rétrécissement améliorera considérablement vos performances, pour très peu de perte en termes de précision dans la plupart des cas.
Maintenant, permet de voir la sortie de l’exécution de ce code., La limite de décision pour l’ensemble de formation ressemble à ceci:

comme nous pouvons le voir et comme nous l’avons appris dans la section Paramètres de réglage, parce que le C a une petite valeur (0.1), la limite de décision est lisse.
maintenant, si nous augmentons le C de 0.,De 1 à 100, nous aurons plus les courbes de la décision de la frontière:

Ce qui se passerait si nous utilisons C=0.1, mais maintenant nous avons augmentation des Gamma de 0,1 à 10? Permet de voir!

Ce qui s’est passé ici? Pourquoi avons-nous un si mauvais modèle?, Comme vous l’avez vu dans la section Paramètres de réglage, un gamma élevé signifie que lors du calcul de l’hyperplan plausible, nous ne considérons que les points proches. Maintenant, comme la densité des points verts n’est élevée que dans la région verte sélectionnée, dans cette région, les points sont suffisamment proches de l’hyperplan plausible, de sorte que ces hyperplans ont été choisis. Soyez prudent avec le paramètre gamma, car cela peut avoir une très mauvaise influence sur les résultats de votre modèle si vous définissez une valeur très élevée (ce qui est une « très grande valeur dépend de la densité des points de données).,
Pour cet exemple, les meilleures valeurs pour C et Gamma 1.0 et 1.0. Maintenant, si nous courons à notre modèle sur l’ensemble de test, nous allons obtenir le schéma suivant:

Et la Confusion de la Matrice ressemble à ceci:

Comme vous pouvez le voir, nous avons seulement 3 Faux Positifs et seulement 4 de Faux Négatifs., La précision de ce modèle est de 93% ce qui est un très bon résultat, nous avons obtenu un meilleur score que l’utilisation de KNN (qui avait une précision de 80%).
remarque: la précision n’est pas la seule mesure utilisée en ML et n’est pas non plus la meilleure mesure pour évaluer un modèle, en raison du paradoxe de la précision. Nous utilisons cette métrique pour la simplicité, mais plus tard, dans le chapitre métriques pour évaluer les algorithmes D’IA, nous parlerons du paradoxe de la précision et je montrerai d’autres métriques très populaires utilisées dans ce domaine.,
Conclusions
dans cet article, nous avons vu un algorithme d’apprentissage supervisé très populaire et puissant, le Support Vector Machine. Nous avons appris l’idée de base, qu’est-ce qu’un hyperplan, quels sont les vecteurs de support et pourquoi sont-ils si importants. Nous avons également vu beaucoup de représentations visuelles, ce qui nous a aidés à mieux comprendre tous les concepts.
un autre sujet important que nous avons abordé est l’Astuce du noyau, qui nous a aidés à résoudre des problèmes non linéaires.
Pour avoir un meilleur modèle, nous avons vu les techniques pour adapter l’algorithme., À la fin de l’article, nous avions un exemple de code en Python, qui nous a montré comment utiliser L’algorithme KNN.
en guise de conclusion, je voudrais donner quelques avantages& inconvénients et quelques cas d’utilisation populaires.,
Pros
- SVN peut être très efficace, car il n’utilise qu’un sous-ensemble des données d’entraînement, seuls les vecteurs de support
- fonctionne très bien sur des ensembles de données plus petits, sur des ensembles de données non linéaires et des espaces dimensionnels élevés
- est très efficace dans les cas où le nombre de dimensions est supérieur au nombre d’échantillons
inconvénients
- Le temps d’entraînement est élevé lorsque nous avons de grands ensembles de données
- lorsque l’ensemble de données a plus de bruit (I.,E. Les classes cibles se chevauchent) SVM ne fonctionne pas bien
cas D’utilisation populaires
- classification de texte
- Détection du spam
- analyse des sentiments
- reconnaissance basée sur les aspects
- reconnaissance basée sur les aspects
- reconnaissance manuscrite de chiffres
