séquence
Une séquence est un ensemble de choses (généralement des nombres) qui sont en ordre.
séquences géométriques
dans une séquence Géométrique, chaque terme est trouvé en multipliant le terme précédent par une constante.
En Général on écrit une Séquence Géométrique comme ceci:
{a, ar, ar2, ar3, …, }
où:
- est le premier terme, et
- r est le facteur entre les deux termes (appelé le « rapport »)
Mais attention, r ne doit pas être 0:
- Lorsque r=0, nous obtenons la séquence {a,0,0,…} qui n’est pas géométrique
la règle
Nous pouvons également calculer n’importe quel terme en utilisant la règle:
xn = ar(n-1)
(Nous utilisons « n-1 » car ar0 est pour le 1er terme)
Une séquence géométrique peut aussi avoir des valeurs de div>
4, 2, 1, 0.5, 0.25, …,
Cette séquence a un facteur de 0,5 (demi) entre chaque numéro.
sa règle est xn = 4 × (0.5)n-1
pourquoi la séquence « Géométrique »?,
Parce que c’est comme l’augmentation des dimensions de la géométrie:
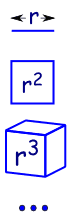 |
une ligne est de dimension 1 et a une longueur de r |
| en 2 dimensions d’un carré a une aire de r2 | |
| en 3 dimensions d’un cube, le volume r3 | |
| etc (oui, on peut avoir plus de 4 dimensions en mathématiques)., |
Les séquences géométriques sont parfois appelées Progressions géométriques (G. P.)
Sommant une série géométrique
pour les additionner:
a + ar + ar2 + … + ar(n-1)
(Chaque terme de l’arche, où k commence à 0 et va jusqu’à n-1)
On peut utiliser cette pratique de formule:

a est le premier terme
r est le « ratio » entre les termes
n est le nombre de termes
Quel est ce drôle de Σ symbole?, Elle est appelée Notation Sigma
| (appelé Sigma) signifie « résumer » |
Et au-dessous et au-dessus sont indiquées les valeurs plancher et plafond:
Il dit: « la Somme des n où n va de 1 à 4. Réponse=10
La formule est facile à utiliser …, juste « plug in » les valeurs de a, r et n
à l’Aide de la Formule
nous allons voir la formule dans l’action:
Exemple: Des Grains de Riz sur un échiquier

Sur la page de Chiffres Binaires nous donner un exemple de grains de riz sur un échiquier. La question est posée:
Quand nous placer le riz sur un échiquier:
- 1 grain sur la première case,
- 2 grains sur la deuxième place,
- 4 grains sur la troisième et ainsi de suite,
- …
… doubler les grains de riz sur chaque carré …
…, combien de grains de riz au total?
nous avons Donc:
- un = 1 (le premier terme)
- r = 2 (double à chaque fois)
- n = 64 (64 cases sur un échiquier)
Donc:

Devient:
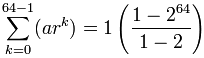
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
ce Qui était exactement le résultat que nous avons obtenu sur les Chiffres Binaires de la page (dieu merci!)
et un autre exemple, cette fois avec r inférieur à 1:
pourquoi la formule fonctionne-t-elle?,
voyons pourquoi la formule fonctionne, car nous utilisons un « truc » intéressant qui mérite d’être connu.
Notez que S et S·r sont semblables?
Maintenant soustraire de!
Wow! Tous les Termes au milieu annulent soigneusement.,
(Qui est un truc intéressant)
En soustrayant S·r de S nous obtenons un simple résultat:
S − S·r = a − arn
nous allons réorganiser pour trouver S:
Qui est notre formule (ta-da!):

série géométrique infinie
alors que se passe-t-il quand n va à l’infini?,
On peut utiliser cette formule:
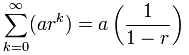
Mais attention:
r doit être entre (non compris) -1 et 1
et r ne doit pas être 0 parce que la séquence {a,0,0,…} n’est pas géométrique
donc notre série géométrique infnite a une somme finie lorsque le rapport est inférieur à 1 (et supérieur à -1)
ramenons notre exemple précédent, et voyons ce qui se passe:
|
Ne me croyez pas? Il suffit de regarder ce carré: en additionnant 12 + 14 + 18 + … Nous nous retrouvons avec le tout!, |
 |
Récurrents Décimal
Sur une autre page, nous avons demandé à « Ne 0.999… égal 1? », Eh bien, voyons si nous pouvons le calculer:



