ANOVA e Tukey test nel software R in pochi passi!

ANOVA noto anche come Analysis of Variance è un potente metodo statistico per testare un’ipotesi che coinvolge più di due gruppi (noti anche come trattamenti). Tuttavia, ANOVA è limitata nel fornire approfondimenti dettagliati tra diversi trattamenti o gruppi, ed è qui che,Tukey (T) test noto anche come T-test entra in gioco. In questo tutorial, vi mostrerò come preparareinput file ed eseguire ANOVA e Tukey test nel software R., Per informazioni dettagliate su ANOVA e R, si prega di leggere questo articolo a questo link.

Fase 1.0 Scaricare e installare il software R e R studio

1. Scaricare e installare l’ultima versione del software R da questo link
2. Scaricare e installare R studio da questo link
3. Infine, installare la libreria qtl in R

Fase 1.,2 – l’Installazione la directory di lavoro seguendo la procedura riportata di seguito:

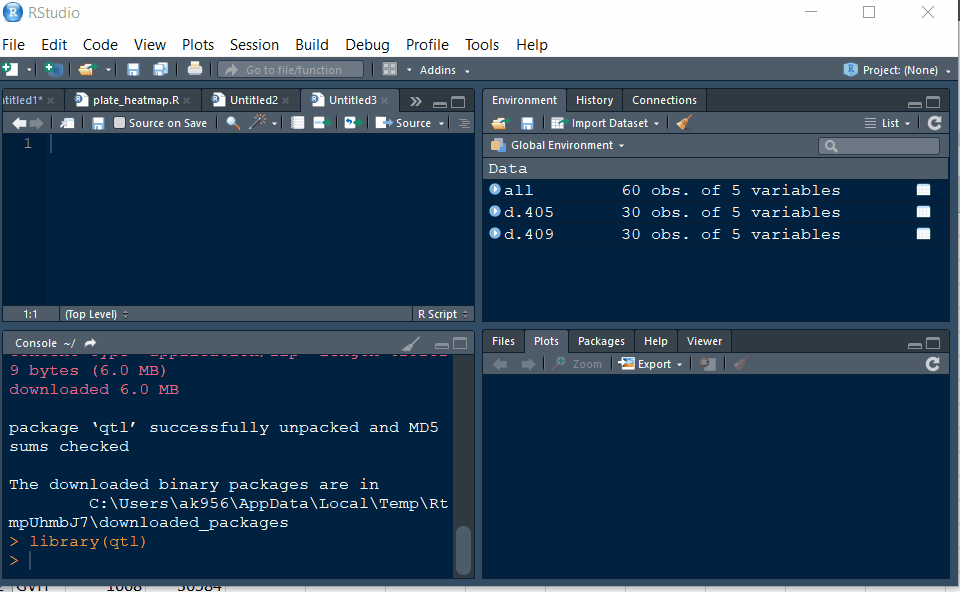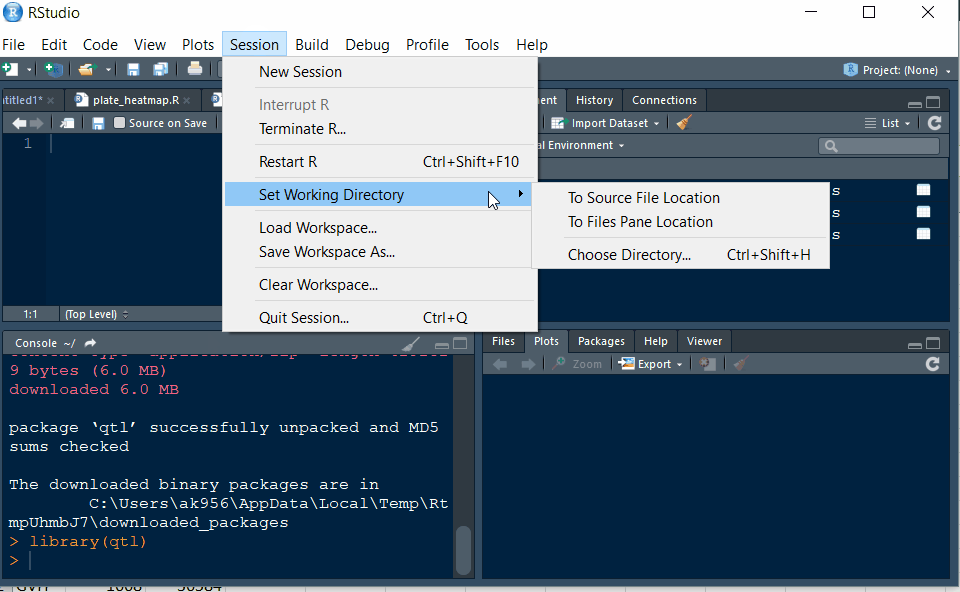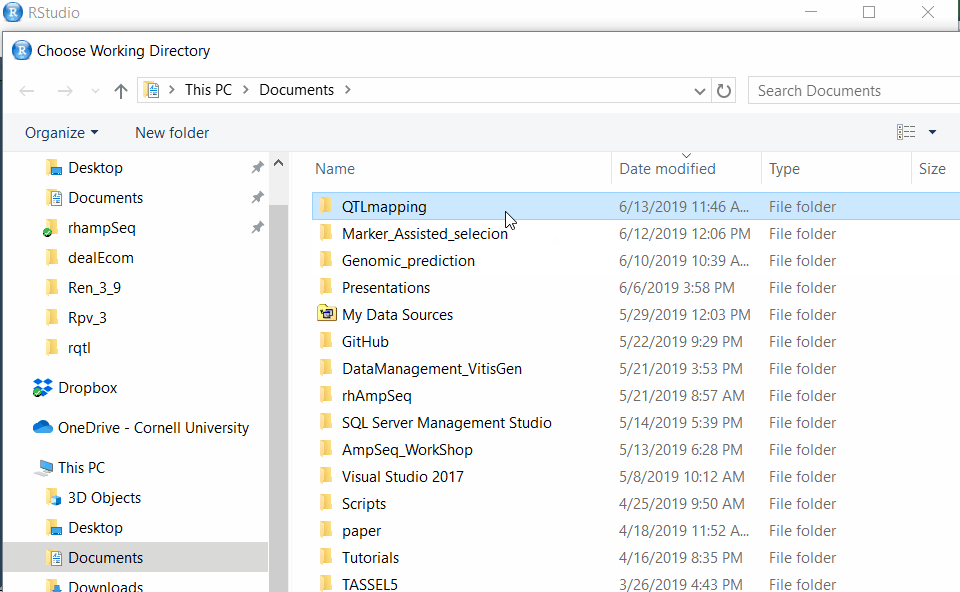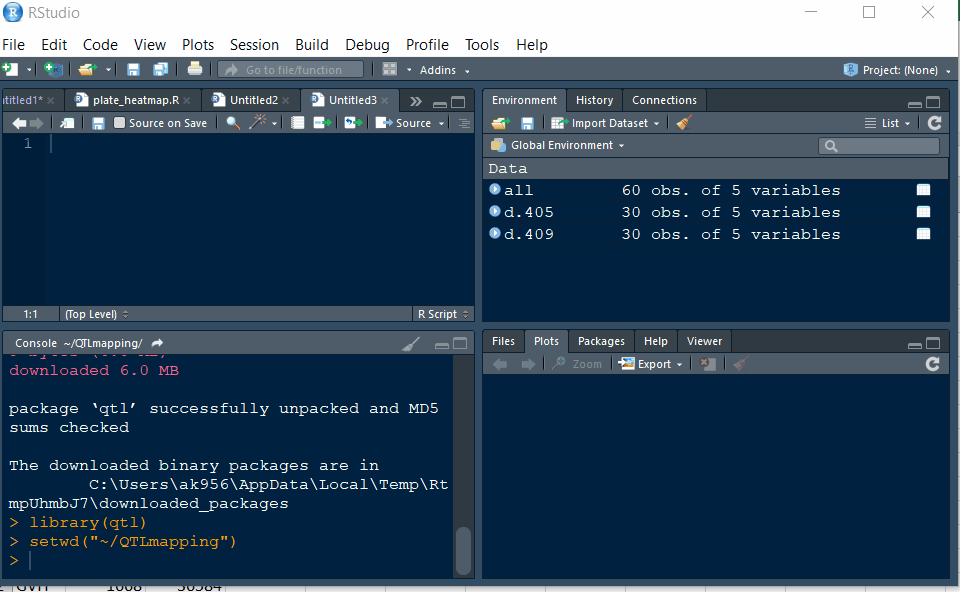
Creare un file di input, come illustrato nell’esempio riportato di seguito:

2.,1 di Importazione pacchetto R

Installare il pacchetto R agricolae e aprire la libreria digitando il seguente comando:

library(agricolae)

Nota: Si prega di ricordarsi di installare il corretto pacchetto R per l’ANOVA!

2.2 Importazione di dati

Importare i dati digitando il seguente comando:

data= read.table(file = "fileName.txt", header = T)

2.3 Controllo dati

una Volta importati i dati, controllare digitando il seguente linea di comando:

head(data_pressure)tail(data_pressure)

2.,4 ANOVA Condotta

Ora, Basta eseguire ANOVA digitando il seguente comando righe:

data.lm <- lm(data$Dependent_variable ~ data$Treatment, data = data)data.av <- aov(data.lm)summary(data.av)

I risultati dovrebbero essere simili, come indicato di seguito:

Dalla sintesi di uscita, si può interpretare che c’è una differenza significativa (cioè P < 0.001) tra i tag Treatments tuttavia, ci perfom di Tukey Test per indagare le differenze tra tutti treaments utilizzando la procedura riportata di seguito.

3.,0 Conduci Tukey test

Digita sotto i comandi per eseguire Tukey test:

data.test <- TukeyHSD(data.av)data.test

0.,001

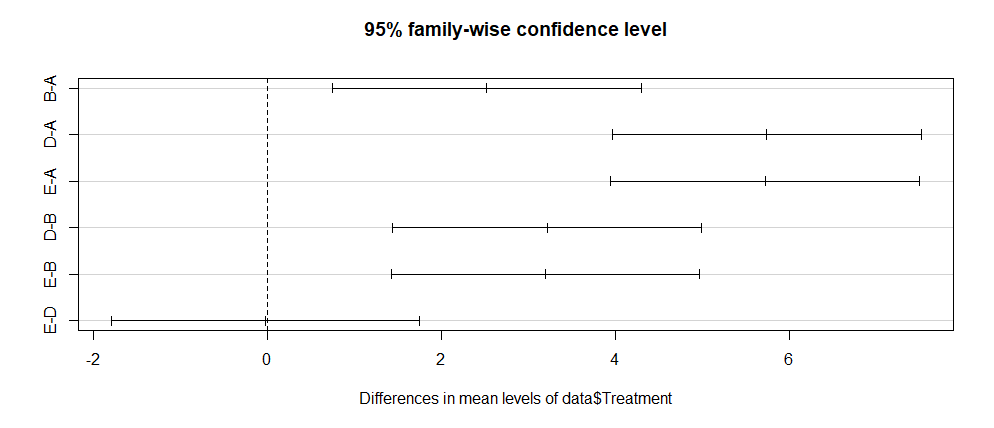
Finally, one can plot the above results using the below command:

plot(data.test)

Output: