Il modo più semplice per catturare l’idea di una popolazione in crescita è con un organismo unicellulare, come un batterio o un cilliate. Nella figura 1, una popolazione di Paramecium in un piccolo vetrino depressione laboratorio è raffigurato. In questa popolazione gli individui si dividono una volta al giorno. Quindi, a partire da un singolo individuo al giorno 0, ci aspettiamo, nei giorni successivi, 2, 4, 8, 16, 32, e 64 individui nella popolazione., Possiamo vedere qui che, in un giorno particolare, il numero di individui nella popolazione è semplicemente il doppio del numero del giorno prima, quindi il numero oggi, chiamalo N (oggi), è uguale al doppio del numero di ieri, chiamalo N(ieri), che possiamo scrivere in modo più compatto come N(oggi) = 2N (ieri).
Quindi ha senso scrivere questo come, N(t) = 2N(t – 1) dove t potrebbe assumere qualsiasi valore.,
Ora possiamo generalizzare un po ‘ questa idea se notiamo che al sesto giorno il numero è uguale al doppio del numero al quinto giorno, o N(6) = 2N(5) e al quinto giorno il numero è uguale al doppio del numero al quarto giorno, o N(5) = 2N(4), ecc.
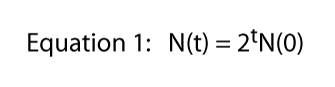
dove t sta per qualsiasi momento (ad esempio, se t = 6, N(6) = 26).
Infine notiamo che questa equazione è stata derivata dalla situazione specifica mostrata in Figura 1, dove una divisione al giorno era la regola dura e veloce., Ecco da dove viene il 2 nell’equazione 1 — da ogni singolo Paramecio otteniamo due individui il giorno successivo. Naturalmente il tasso di divisione potrebbe essere qualsiasi cosa. Se ci fossero due divisioni al giorno ma una cellula morisse sempre, ci aspetteremmo tre individui da ogni singolo individuo e l’equazione 1 sarebbe N(t) = 3tN(0)., Così il tasso di divisione potrebbe essere un qualsiasi numero e l’equazione generale diventa,
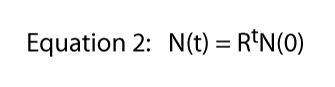
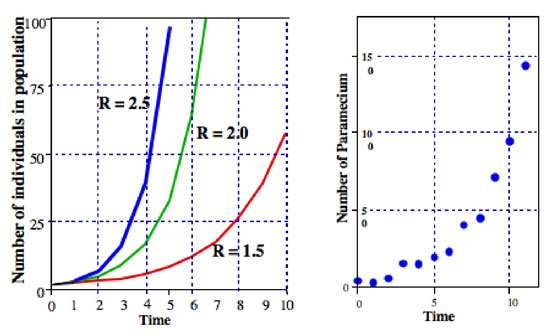
dove R è di solito chiamato il finito, il tasso di incremento demografico (nel caso concreto della divisione Paramecium finito il tasso di incremento della popolazione, è pari a divisione di frequenza). Nella Figura 2 illustriamo questa equazione per vari valori di R. Normalmente viene definita equazione esponenziale e la forma dei dati in Figura 2 è la forma generale chiamata esponenziale.,
Qualsiasi valore di R può essere rappresentato in un numero infinito di modi (ad esempio, se R = 16, potremmo scrivere R = 8 x 2, o R = 42, o R = 32/2, o R = 2.718282.77). Quest’ultima espressione (R = 2.718282.,77) fa uso di una costante importante che potrebbe essere richiamata dal calcolo elementare, la costante di Eulero. Esprimere qualsiasi valore di R come costante di Eulero elevato a una certa potenza è in realtà estremamente utile-porta tutta la potenza del calcolo nell’immagine.,olize costante di Eulero e possiamo scrivere l’Equazione di 2
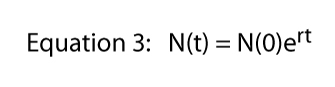
Ora, se prendiamo il logaritmo naturale di entrambi i lati dell’Equazione 3 — ricordare ln(ex) = x — Equazione 3 diventa: ln = ln + rt
E se abbiamo iniziato la popolazione con un singolo individuo (come nell’esempio sopra), abbiamo

dalla quale si vede che il logaritmo naturale della popolazione, in un determinato momento, è una costante, i tempi di quel tempo., La costante r è indicata come il tasso intrinseco di aumento naturale (Figura 2).
Tutti i tipi di microrganismi mostrano modelli molto vicini alla crescita esponenziale della popolazione. Ad esempio, nel grafico a destra della figura 2 è una popolazione di Paramecium che cresce in una coltura di laboratorio. Il modello di crescita è molto vicino al modello dell’equazione esponenziale.
Un altro modo di scrivere l’equazione esponenziale è come un’equazione differenziale, cioè rappresenta la crescita della popolazione nella sua forma dinamica., Invece di chiedere che cosa è la dimensione della popolazione al tempo t, ci chiediamo, che cosa è il tasso al quale la popolazione è in crescita al tempo t. Il tasso è simboleggiato dN/dt, che significa semplicemente “variazione N rispetto al cambiamento in t”, e se richiamo la vostra base di calcolo, siamo in grado di trovare il tasso di crescita, differenziando l’Equazione 4, che ci dà
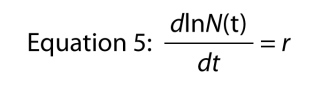
il che è notevole, perché si dice che il tasso di crescita del log del numero della popolazione è costante., Quel tasso costante di crescita del registro della popolazione è il tasso intrinseco di aumento.,
Ricordiamo che il tasso di cambio del logaritmo di un numero è lo stesso come il “pro capite” variazione di tale numero, il che significa che si può scrivere l’Equazione 5

in cui si omette la variabile t è ovvio dove si va, e poi ci riorganizzare un po ‘ a venire con
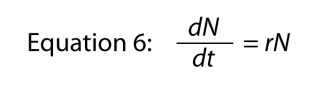
in cui il parametro r è, di nuovo, il tasso intrinseco di crescita naturale., La relazione di base tra tasso finito di aumento e tasso intrinseco è
r = ln(R)
dove ln si riferisce al logaritmo naturale. Si noti che l’equazione 6 e l’equazione 3 sono solo forme diverse della stessa equazione (l’equazione 3 è la forma integrata dell’equazione 6; L’equazione 6 è la forma differenziata dell’equazione 3), ed entrambe possono essere definite semplicemente come l’equazione esponenziale.,

L’equazione esponenziale è un modello utile di popolazioni semplici, almeno per periodi di tempo relativamente brevi., Ad esempio, se un tecnico di laboratorio deve sapere quando una coltura batterica raggiunge una certa densità di popolazione, l’equazione esponenziale può essere utilizzata per fornire una previsione su quando esattamente verrà raggiunta quella dimensione della popolazione. Un altro esempio è nel caso dei parassiti agricoli. Gli erbivori sono sempre potenzialmente grandi problemi per le piante. Quando le piante sottoposte a tali focolai sono agricole, vale a dire colture, la perdita può essere molto significativa sia per l’agricoltore che per il consumatore. Quindi, c’è sempre pressione per prevenire tali epidemie., Dalla seconda guerra mondiale l’arma principale nella lotta contro tali epidemie di parassiti è stata pesticidi chimici, come il DDT. Tuttavia, negli ultimi anni ci siamo resi conto che questi pesticidi sono estremamente pericolosi nel lungo periodo, sia per l’ambiente che per le persone. Di conseguenza c’è stato un movimento per limitare la quantità di pesticidi che vengono spruzzati per combattere i parassiti. Il modo principale per farlo è stabilire una soglia economica, che è la densità di popolazione del potenziale parassita al di sotto della quale il danno alla coltura è insignificante (cioè, non è realmente necessario spruzzare)., Quando la popolazione di parassiti aumenta al di sopra di tale soglia, l’agricoltore deve agire e applicare una sorta di pesticida o altri mezzi per controllare il parassita. Data la natura di questo problema, a volte è della massima importanza essere in grado di prevedere quando il parassita raggiungerà la soglia economica. Conoscere la R per le specie di parassiti consente all’agricoltore di prevedere quando sarà necessario applicare una sorta di procedura di controllo (Figura 3).
L’equazione esponenziale è anche un modello utile per sviluppare idee intuitive sulle popolazioni., L’esempio classico è uno stagno con una popolazione di ninfee. Se ogni ninfea si riproduce (due pastiglie prendono il posto di dove un pad era stato) ogni mese, e ci sono voluti, diciamo, tre anni per lo stagno per diventare mezzo pieno di ninfee, quanto tempo ci vorrà per lo stagno per essere completamente coperto con ninfee? Se non ci si ferma a pensare troppo chiaramente, si è tentati di dire che ci vorrà altrettanto tempo, tre anni, perché la seconda metà dello stagno diventi piena come la prima. La risposta, ovviamente, è di un mese.,
Un altro esempio popolare è il proverbiale antico matematico egiziano (o talvolta persiano) che chiede il pagamento dal re sotto forma di chicchi di grano (a volte riso). Un grano sul primo quadrato di una scacchiera, due grani sul secondo quadrato, e così via, fino all’ultimo quadrato. Il Faraone non può immaginare che un pagamento così semplice potrebbe ammontare a molto, e così è d’accordo. Ma non ha pienamente apprezzato la crescita esponenziale., Poiché ci sono 64 quadrati sulla scacchiera, possiamo usare l’equazione 2 per determinare quanti chicchi di grano saranno tenuti a pagare sull’ultimo quadrato (R elevato alla 64a potenza, che è di circa 18.446.744.074.000.000.000 — un sacco di grano davvero, certamente più che in tutto il regno). Questi esempi sottolineano il modo spesso sorprendente in cui un processo esponenziale può portare a numeri molto grandi molto rapidamente.
