Risposta:
Per un triangolo retto:

La funzione seno il peccato toglie angolo θ e dà il rapporto di fronte ipotenusa
L’inverso della funzione sinusoidale peccato-1 prende il rapporto oppositehypotenuse e dà angolo θ
E coseno e tangente di seguire una simile idea.,
E ora per i dettagli:
Seno, Coseno e Tangente sono tutti basati su un triangolo rettangolo
Sono funzioni molto simili … quindi guarderemo la Funzione Seno e poi il Seno inverso per imparare di cosa si tratta.,
Funzione Sinusoidale
Il Seno dell’angolo θ è:
- la lunghezza del lato Opposto angolo θ
- diviso per la lunghezza dell’Ipotenusa
O più semplicemente:
sin(θ) = Opposto / Ipotenusa
La Funzione del Seno può aiutare a risolvere cose come questa:
arcoseno Funzione
Ma a volte è l’angolo che abbiamo bisogno di trovare.
Questo è dove “Seno inverso” entra in gioco.
Risponde alla domanda ” quale angolo ha seno uguale a opposto / ipotenusa?,”
Il simbolo per il seno inverso è sin-1, o talvolta arcsin.
Sono come avanti e indietro!

- sin prende un angolo e ci dà il rapporto “opposto/ipotenusa”
- sin-1 prende il rapporto “opposto / ipotenusa” e ci dà l’angolo.
Esempio:
Calcolatrice
 |
calcolatrice premere uno dei seguenti (a seconda della marca di calcolatrice):o ‘2ndF peccato” o “shift peccato’. |
Sulla tua calcolatrice, prova a usare sin e poi sin-1 per vedere cosa succede
Più di un angolo!
Il seno inverso mostra solo un angolo … ma ci sono più angoli che potrebbero funzionare.
Esempio: Ecco due angoli dove opposto / ipotenusa = 0.,5
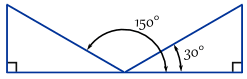
In effetti ci sono infiniti angoli, perché puoi continuare ad aggiungere (o sottrarre) 360°:
Ricorda questo, perché ci sono momenti in cui hai effettivamente bisogno di uno degli altri angoli!
Sommario
Il Seno dell’angolo θ è:
sin(θ) = Opposto / Ipotenusa
E l’arcoseno è :
sin-1 (Opposto / Ipotenusa) = θ
che Cosa Circa “cos” e “tan” … ?
Esattamente la stessa idea, ma diversi rapporti laterali.,
Coseno
Il Coseno dell’angolo θ è:
cos(θ) = Adiacente / Ipotenusa
E Coseno Inverso :
cos-1 (Adiacente / Ipotenusa) = θ
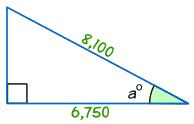
Esempio: Trovare la misura dell’angolo°
cos a° = Adiacente / Ipotenusa
cos a° = 6,750/8,100 = 0.8333…
a° = cos-1 (0,8333…) = 33.,6° (a 1 decimale)
Tangente
La Tangente dell’angolo θ è:
tan(θ) = Fronte / Adiacente
Tangente Inversa è :
tan-1 (Fronte / Adiacente) = θ
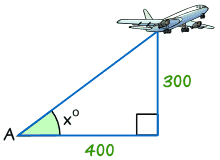
Esempio: Trovare la misura dell’angolo x°
tan x° = Fronte / Adiacente
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (giusto per 1 decimale)
Altri Nomi
a Volte il peccato-1 è chiamato asin o arcsin
allo stesso modo cos-1 è chiamato oac o arccos
E tan-1 è chiamato atan o arctan
Esempi:
- arcsin(y) è la stessa sin-1(y)
- atan(θ) è lo stesso come tan-1(q)
- etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- Ma il Seno inverso e il coseno inverso non “vanno avanti per sempre” come fanno Seno e coseno …
Diamo un’occhiata all’esempio del Coseno.
Ecco Seno e Coseno Inverso tracciate sullo stesso grafico:
Coseno e Coseno Inverso
sono immagini speculari (sulla diagonale)
Ma perché arcocoseno ottenere tagliato in alto e in basso (i punti non sono realmente parte della funzione) … ?
Perché per essere una funzione può dare solo una risposta
quando chiediamo ” cos’è cos-1 (x) ?,”
Una risposta o infinite risposte
Ma abbiamo visto prima che ci sono infinite risposte, e la linea tratteggiata sul grafico lo mostra.
Quindi sì, ci sono infinite risposte …
… ma immagina di digitare 0.5 nella tua calcolatrice, premere cos-1 e ti dà una lista infinita di possibili risposte …
Quindi abbiamo questa regola che una funzione può dare solo una risposta.
Quindi, tagliandolo via in questo modo otteniamo solo una risposta, ma dovremmo ricordare che potrebbero esserci altre risposte.,
Tangente e tangente inversa
Ed ecco la funzione tangente e tangente inversa. Si può vedere come sono immagini speculari (circa la diagonale) …?

Tangente

Tangente Inversa



