Sequenza
Una sequenza è un insieme di cose (di solito numeri) che sono in ordine.
Sequenze geometriche
In una Sequenza geometrica ogni termine viene trovato moltiplicando il termine precedente per una costante.
In generale scriviamo una Sequenza geometrica come questa:
{a, ar, ar2, ar3, …, }
dove:
- a è il primo termine e
- r è il fattore tra i termini (chiamato “rapporto comune”)
Ma attenzione, r non dovrebbe essere 0:
- Quando r=0, otteniamo la sequenza {a, 0,0,…} che non è geometriche
La Regola
Possiamo anche calcolare qualsiasi termine utilizzando la Regola:
xn = ar(n-1)
(usiamo “n-1” perché ar0 è per il 1 ° termine)
Una Sequenza Geometrica può avere anche più piccoli valori:
Esempio:
4, 2, 1, 0.5, 0.25, …,
Questa sequenza ha un fattore di 0,5 (mezzo) tra ogni numero.
La sua regola è xn = 4 × (0,5)n-1
Perché sequenza “geometrica”?,
Perché è come aumentare le dimensioni in geometria:
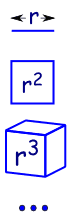 |
linea 1-dimensionale e ha una lunghezza di r |
| in 2 dimensioni di un quadrato ha una superficie di r2 | |
| in 3 dimensioni di un cubo di volume r3 | |
| ecc (sì, si può avere 4 o più dimensioni in matematica)., |
Le sequenze geometriche sono talvolta chiamate Progressioni geometriche (GP’s)
Sommando una serie geometrica
Per sommare queste:
a + ar + ar2 + … + ar(n-1)
(Ogni termine è arca, dove k inizia a 0 e va fino a n-1)
E ‘ possibile utilizzare questo comodo formula:

è il primo termine
r è il “rapporto” tra i termini
n è il numero di termini
che Cosa è divertente Σ simbolo?, Si chiama Sigma Notazione
| (Sigma) significa “riassumere” |
e al di sotto E al di sopra di essa sono riportati i valori iniziale e nale:
Si dice “Somma di n, dove n va da 1 a 4. Risposta=10
La formula è facile da usare …, “plug in” valori di a, r e n
Utilizzando la Formula
vediamo la formula in azione:
Esempio: Chicchi di Riso su una scacchiera

Sulla pagina Cifre Binarie diamo un esempio di chicchi di riso su una scacchiera. La domanda è posta:
Quando mettiamo il riso su una scacchiera:
- 1 grano sul primo quadrato,
- 2 grani sul secondo quadrato,
- 4 grani sul terzo e così via,
- …
… raddoppiando i chicchi di riso su ogni quadrato …
…, quanti chicchi di riso in totale?
ci sono due possibilità:
- a = 1 (primo termine)
- r = 2 (raddoppia ogni volta)
- n = 64 (64 quadrati, su una scacchiera)
Così:

Diventa:
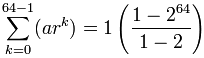
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Che è esattamente il risultato che abbiamo ottenuto per le Cifre Binarie pagina (grazie al cielo!)
E un altro esempio, questa volta con r inferiore a 1:
Perché la Formula funziona?,
Vediamo perché la formula funziona, perché possiamo usare un interessante “trucco” che vale la pena conoscere.
Si noti che S e S·r sono simili?
Ora sottraili!

Wow! Tutti i termini nel mezzo si annullano ordinatamente.,
(Che è un trucchetto:)
sottraendo S·r, S, otteniamo un risultato semplice:
S − S·r = a − arn
proviamo a riorganizzare per trovare S:
Che è la nostra formula (ta-da!):

Serie geometrica infinita
Quindi cosa succede quando n va all’infinito?,
Possiamo usare questa formula:
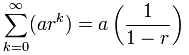
Ma fai attenzione:
r deve essere compreso tra (ma non incluso) -1 e 1
e r non dovrebbe essere 0 perché la sequenza {a,0,0,…} non è geometrico
Quindi la nostra serie geometrica infnite ha una somma finita quando il rapporto è inferiore a 1 (e maggiore di -1)
Riportiamo il nostro esempio precedente e vediamo cosa succede:
|
Non mi credi? Basta guardare questo quadrato: sommando 12 + 14 + 18 + … finiamo con il tutto!, |
 |
Decimale ricorrente
In un’altra pagina abbiamo chiesto “Fa 0.999… uguale a 1?”, beh, vediamo se possiamo calcolarlo:


