Coefficiente di correlazione
Quanto bene la tua equazione di regressione rappresenta veramente
il tuo set di dati?
Uno dei modi per determinare la risposta a questa domanda è quello di
esame il coefficiente di correlazione e il coefficiente di determinazione.,
|
|
Il coefficiente di correlazione, r, e |
Oltre ad apparire con le informazioni di regressione, i valori rand r 2 possono essere trovati underVARS, #5 Statistics → EQ #7 r e #8 r 2 .,
Coefficiente di correlazione, r:
La quantità r, chiamata coefficiente di correlazione lineare, misura la forza e
la direzione di una relazione lineare tra due variabili. Il coefficiente di correlazione lineare
è talvolta indicato come il coefficiente di correlazione momento prodotto Pearson in
onore del suo sviluppatore Karl Pearson.La formula matematica per computingr è: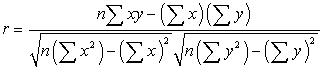
dove n è il numero di coppie di dati.,
(Non sei contento di avere una calcolatrice grafica che calcola questa formula?) Il valore di r è tale che -1< r< +1. I segni + e – sono usati rispettivamente per correlazioni lineari positive
e correlazioni lineari negative. Correlazione positiva: se x e y hanno una forte correlazione lineare positiva,r è vicino
a +1. Un valore r esattamente + 1 indica una perfetta vestibilità positiva., Valori positivi
indicano una relazione tra le variabili x e y tale che, quando i valori per x aumentano, anche i valori per y aumentano. Correlazione negativa: se x e y hanno una forte correlazione lineare negativa,r è vicino
a -1. Un valore r di esattamente -1 indica un perfetto adattamento negativo. Valori negativi
indicano una relazione tra x e y tale che, come i valori per x aumentano, i valori
per y diminuiscono.
Nessuna correlazione: se non esiste una correlazione lineare o una correlazione lineare debole, r è
vicino a 0., Un valore vicino a zero significa che esiste una relazione casuale, non lineare
tra le due variabili Si noti che r è una quantità adimensionale; cioè, non dipende dalle unità
impiegate.Una correlazione perfetta di ± 1 si verifica solo quando i punti dati si trovano tutti esattamente su una
linea retta. Se r = + 1, la pendenza di questa linea è positiva. Se r = -1, la pendenza di questa linea
è negativa. Una correlazione maggiore di 0.8 è generalmente descritta come forte, mentre una correlazione
minore di 0.,5 è generalmente descritto comedebole. Questi valori possono variare in base al
“tipo” di dati in esame. Uno studio che utilizza dati scientifici può richiedere una correlazione più forte di uno studio che utilizza dati di scienze sociali.
Coefficiente di Determinazione r 2 o R2 :
Il coefficiente di determinazione r 2,è utile perché dà la percentuale di
la varianza (fluttuazione) di una variabile che è prevedibile l’altra variabile.,
Si tratta di una misura che ci permette di determinare come uno certo può essere nel fare
previsioni da un certo modello/grafico.
Il coefficiente di determinazione è il rapporto tra la variazione spiegata e la variazione totale
.
Il coefficiente di determinazione è tale che 0<r 2<1, e denota la forza
dell’associazione lineare tra x e y., Il coefficiente di determinazione rappresenta la percentuale dei dati che è il più vicino
alla linea di best fit. Ad esempio, se r = 0,922, allora r 2 = 0,850, il che significa che
l ‘ 85% della variazione totale iny può essere spiegato dalla relazione lineare tra x
e y (come descritto dall’equazione di regressione). L’altro 15% della variazione totale
in y rimane inspiegabile.
Il coefficiente di determinazione è una misura di quanto bene la linea di regressione
rappresenta i dati., Se la linea di regressione passa esattamente attraverso ogni punto del grafico a dispersione, sarebbe in grado di spiegare tutte le variazioni. Più la linea è lontana dai punti, meno è in grado di spiegare.