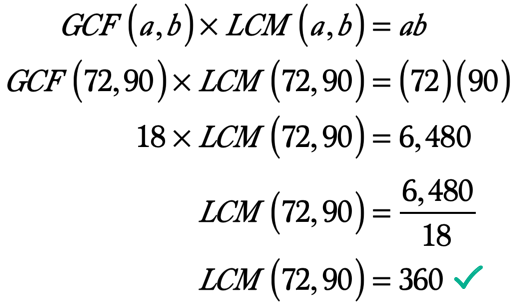Kiedy badałeś, jak znaleźć GCF i LCM dwóch liczb dodatnich, czy odkryłeś bardzo interesującą zależność między tymi dwoma wielkościami?

zrobiłem! Odkryłem to przez przypadek, kiedy byłem młodym studentem i myślałem, że natknąłem się na coś, co było „rewolucyjne”. Byłem tak podekscytowany, że podzieliłem się tym z moim nauczycielem., Ale ku mojej frustracji spojrzał mi w oczy i powiedział, że to już udowodnione twierdzenie matematyczne. Poczułem się zniechęcony na chwilę, ale wróciłem do pracy w szkole i naciskałem.

Jeśli jeszcze go nie napotkałeś, istnieje niezwykła zależność algebraiczna lub związek między największym wspólnym czynnikiem (GCF) a najmniejszą wspólną wielokrotnością (LCM) dwóch liczb. W tej lekcji, liczby, które chcemy, to te należące tylko do zbioru dodatnich liczb całkowitych.,
Poniżej znajduje się algebraiczny związek pomiędzy GCF i LCM dwóch dodatnich liczb całkowitych.
formuła GCF-LCM
Ostrzeżenie: naprawdę nie ma czegoś takiego jak „Formuła GCF-LCM”. Wymyśliłem nazwę dla ułatwienia odniesienia. Możesz nazywać to jak chcesz, o ile służy swojemu celowi.,
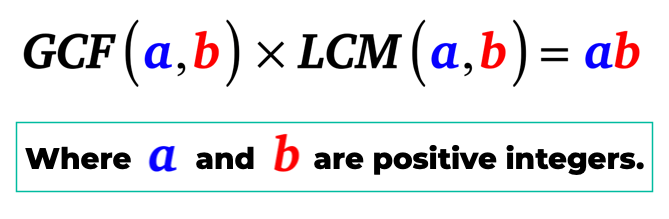
Mówiąc najprościej, największy wspólny współczynnik a i B po pomnożeniu do najmniejszej wspólnej wielokrotności a i b jest równy iloczynowi a i B. to znaczy, a i B są dodatnimi liczbami całkowitymi.
przykładowe problemy
przykład 1: GCF z 12 i 16 wynosi 4. Co to jest LCM z 12 i 16?
możesz określić LCM z 12 i 16 za pomocą jednej z dwóch poniższych metod.,
- znalezienie LCM przy użyciu metody List
- znalezienie LCM przy użyciu metody faktoryzacji Prime
istnieje jednak znacznie szybszy sposób. Możesz skorzystać z „Formuły GCF-LCM”, ponieważ znasz dwie liczby całkowite i jej GCF. Wystarczy podłączyć wartości do formuły, a następnie rozwiązać dla LCM.
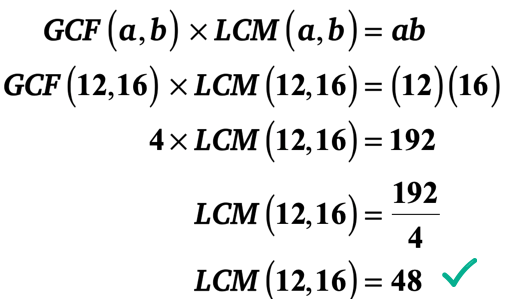
pozostawiam Ci sprawdzenie, czy LCM z 12 i 16 jest rzeczywiście 48.
przykład 2: LCM z 24 i 40 wynosi 120. Co to jest GCF 24 i 40?,
Ten problem jest dokładnym przeciwieństwem przykładu 1, ponieważ podano wartość LCM zamiast GCF.
czyli takie informacje znamy. Podzielmy je dla jasności.
▶▶ LCM(24,40) = 120
▶ ▶ a=24 i b=40 dlatego ab = \left( {24} \right)\left( {40} \right) = 960
▶ uwaga: nie ma znaczenia, które liczby są a i b. nie zmieni to wyniku ostatecznej odpowiedzi. Jednak jest to dobra praktyka standaryzacji rozwiązania. Sugeruję, aby a było mniejszą liczbą całkowitą, podczas gdy b było większą liczbą całkowitą.,
podstawimy znane wartości do wzoru, a następnie rozwiążmy dla GCF 24 i 40.
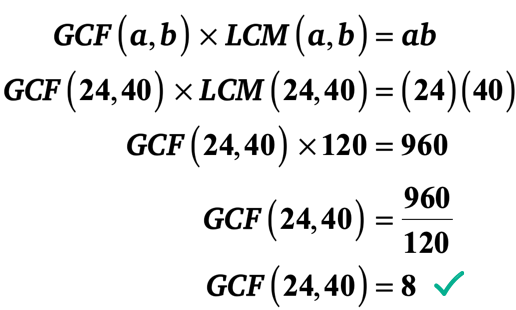
przykład 3: Znajdź GCF 20 i 25, najpierw obliczając LCM 20 i 25.
ten problem będzie nieco inny niż przykłady #1 i # 2. Najpierw musisz obliczyć najmniejszą wspólną wielokrotność (LCM) 20 i 25. Następnie można rozwiązać dla największego wspólnego czynnika (GCF) 20 i 25 za pomocą wzoru GCF-LCM.
no to zaczynamy!, Aby znaleźć LCM 20 i 25, napiszemy kilka pierwszych wielokrotności 20 i 25. Pierwszą wspólną wielokrotnością, która się pojawi, będzie nasz LCM.
20: 20, 40, 60, 80, 100, 120
wielokrotności 25: 25, 50, 75, 100, 125, 150
ponieważ liczba 100 pojawia się jako pierwsza wspólna wielokrotność 20 i 25, możemy twierdzić, że LCM 20 i 25 wynosi 100.
mamy teraz wszystkie informacje, aby użyć formuły. Poniżej znajdują się wartości, które zamierzamy zastąpić wzorem do rozwiązania dla LCM 20 i 25.,
product iloczyn a i b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ LCM 20 i 25 → LCM\left( {20,25} \right) = 100
oto obliczenia do rozwiązania dla GCF 20 i 25:
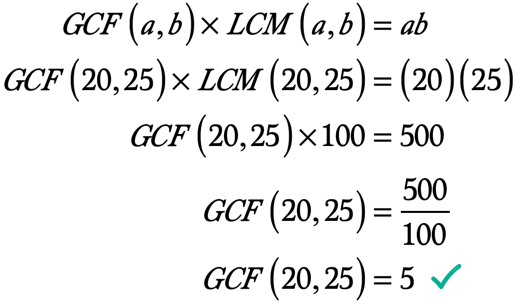
przykład 4: Znajdź LCM z 63 I 84, najpierw obliczając GCF z 63 I 84.
Ten problem jest bardzo podobny do przykładu #3. Jedyną różnicą jest to, że najpierw obliczysz GCF zamiast LCM, zgodnie z instrukcjami samego problemu.,
znajdźmy wszystkie czynniki 63 I 84. Możesz użyć techniki” rainbow method ” do uwzględnienia podanych liczb całkowitych.
zauważ, że największy lub najwyższy współczynnik wspólny między dwiema listami wynosi 21.
63: 1, 3, 7, 9, 21, 63
84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
dlatego największym wspólnym czynnikiem 63 I 84 jest 21. Tak więc GCF \ left ({63,84} \ right) = 21.,
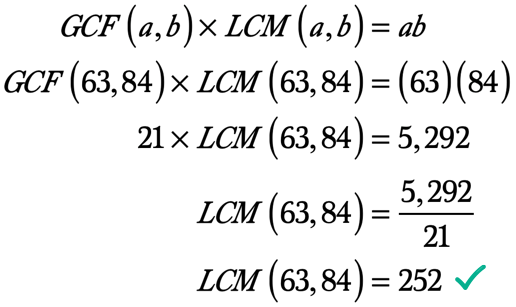
przykład 5: Znajdź LCM z 72 i 90 za pomocą wzór GCF-LCM.
jak już wiemy, możemy znaleźć LCM dwóch liczb całkowitych o wartości jego GCF za pomocą wzoru GCF-LCM.,
wymieniając zarówno czynniki 72 jak i 90 mamy:
wszystkie czynniki 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
wszystkie czynniki 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Kiedy porównujemy listy czynników, widzimy, że 18 jest czynnikiem, który jest wspólny dla obu, ale ma największą lub największą wartość. Oznacza to, że GCF 72 i 90 wynosi 18, czyli GCF \ left ({72,90} \right) = 18.
jesteśmy teraz gotowi zastąpić poniższe wartości w formule.,
ab ab = \left ({72} \ right) \ left ({90} \ right) = 6480
❖ GCF\left( {72,90} \right) = 18
oto obliczenie, aby znaleźć LCM, biorąc pod uwagę, że znamy już GCF dwóch liczb całkowitych i ich iloczyn.