najprostszym sposobem na uchwycenie idei rosnącej populacji jest jednokomórkowy organizm, taki jak bakteria lub cilliate. Na rysunku 1 przedstawiono populację Paramecium w małej laboratoryjnej zjeżdżalni depresji. W tej populacji osobniki dzielą się raz na dobę. Tak więc, zaczynając od jednej osoby w dniu 0, spodziewamy się, w kolejnych dniach, 2, 4, 8, 16, 32, i 64 osoby w populacji., Widzimy tutaj, że w danym dniu liczba osób w populacji jest po prostu dwa razy większa niż liczba poprzedniego dnia, więc liczba dzisiaj, nazwij ją N (dzisiaj), jest równa dwukrotności liczby wczoraj, nazwij ją N (wczoraj), którą możemy napisać bardziej zwięźle jako N (dzisiaj) = 2N (wczoraj).
więc sensowne jest zapisanie tego jako, N(t) = 2n(t – 1), Gdzie t może przyjąć dowolną wartość w ogóle.,
teraz możemy nieco uogólnić ten pomysł, jeśli zauważymy, że w dniu szóstym liczba jest równa dwukrotności liczby w dniu piątym, lub N(6) = 2N(5), a w dniu piątym liczba jest równa dwukrotności liczby w dniu czwartym, lub N(5) = 2N(4), itd.
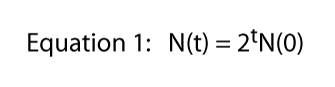
gdzie t oznacza Dowolny czas (np. jeśli t = 6, N(6) = 26).
wreszcie zauważamy, że równanie to zostało wyprowadzone z konkretnej sytuacji pokazanej na rysunku 1, gdzie jeden podział na dzień był regułą twardą i szybką., Stąd bierze się 2 w równaniu 1 — z każdego pojedynczego Paramecium otrzymujemy dwa osobniki następnego dnia. Oczywiście Współczynnik podziału może być dowolny. Gdyby były dwa podziały dziennie, ale jedna komórka zawsze umierała, spodziewalibyśmy się trzech osobników z każdego pojedynczego osobnika, a równanie 1 byłoby N(t) = 3TN (0)., Tak więc współczynnik podziału może być dowolną liczbą, a ogólne równanie staje się,
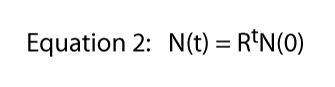
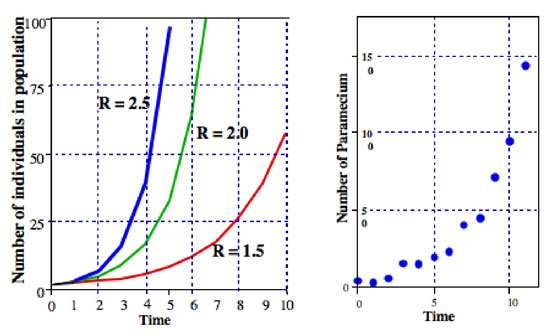
gdzie R jest zwykle nazywany skończoną szybkością wzrostu populacji (w faktycznym przypadku dzielenia Paramecium wskaźnik wzrostu populacji jest równy wskaźnikowi podziału). Na rysunku 2 zilustrujemy to równanie dla różnych wartości R. zwykle nazywa się je równaniem wykładniczym, a postać danych na rysunku 2 jest ogólną formą zwaną wykładniczym.,
dowolna wartość R może być reprezentowana na nieskończoną liczbę sposobów (np. jeśli R = 16, możemy zapisać R = 8 x 2, lub R = 42, lub r = 32/2, lub r = 2.718282.77). To ostatnie wyrażenie (R = 2.718282.,77) wykorzystuje ważną stałą, którą można przywołać z rachunku elementarnego, stałą Eulera. Wyrażenie dowolnej wartości R jako stałej Eulera podniesionej do pewnej potęgi jest w rzeczywistości niezwykle użyteczne — przynosi pełną moc rachunku różniczkowego do obrazu.,stała Eulera jako E możemy zapisać równanie 2 jako
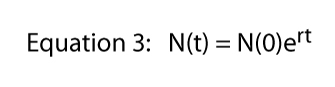
teraz jeśli weźmiemy log naturalny obu stron równania 3 — pamiętaj ln(ex) = X — równanie 3 staje się: Ln = LN + RT
i jeśli rozpoczęliśmy populację od jednej osoby (jak w powyższym przykładzie), mamy

od który widzimy, że naturalny dziennik populacji, w danym czasie, jest jakiś stały, razy w tym czasie., Stała r jest określana jako wewnętrzna szybkość naturalnego wzrostu (Rys. 2).
wszelkiego rodzaju mikroorganizmy wykazują wzorce zbliżone do wykładniczego wzrostu populacji. Na przykład na wykresie po prawej stronie rysunku 2 znajduje się populacja Paramecium rosnąca w kulturze laboratoryjnej. Wzór wzrostu jest bardzo zbliżony do wzoru równania wykładniczego.
innym sposobem zapisu równania wykładniczego jest równanie różniczkowe, czyli reprezentujące wzrost populacji w jej dynamicznej postaci., Zamiast pytać, jaka jest wielkość populacji w czasie t, pytamy, jaka jest szybkość, z jaką populacja rośnie w czasie t. tempo jest symbolizowane jako DN/dt, co po prostu oznacza „zmiana w N w stosunku do zmiany w t”, a jeśli przypomnisz sobie swoje podstawowe obliczenia, możemy znaleźć tempo wzrostu poprzez różnicowanie równania 4, co daje nam
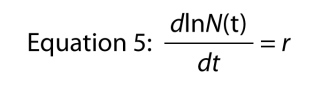
Co jest dość niezwykłe, ponieważ mówi, że tempo wzrostu logu liczby w populacji jest stała., Ta stała szybkość przyrostu liczby ludności jest nieodłączną szybkością przyrostu.,
Przypomnijmy, że szybkość zmiany dziennika liczby jest taka sama jak zmiana „na mieszkańca” w tej liczbie, co oznacza, że możemy zapisać równanie 5 jako

gdzie pomijamy zmienną t, ponieważ jest oczywiste, gdzie idzie, a następnie zmieniamy bit, aby wymyślić
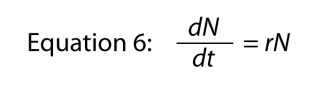
gdzie parametr R jest, ponownie, parametrem wrodzona szybkość naturalnego wzrostu., Podstawową relacją między stopniem wzrostu skończonego a stopniem wzrostu wewnętrznego jest
r = ln(R)
Gdzie LN odnosi się do logarytmu naturalnego. Należy zauważyć, że równanie 6 I równanie 3 są po prostu różnymi postaciami tego samego równania (równanie 3 jest zintegrowaną formą równania 6; równanie 6 jest zróżnicowaną formą równania 3), a oba mogą być określane po prostu jako równanie wykładnicze.,

równanie wykładnicze jest użytecznym modelem prostych populacji, przynajmniej przez stosunkowo krótkie okresy czasu., Na przykład, jeśli Technik laboratoryjny musi wiedzieć, kiedy kultura bakteryjna osiąga pewną gęstość zaludnienia, wykładnicze równanie może być używany do zapewnienia przewidywania, kiedy dokładnie wielkość populacji zostanie osiągnięty. Inny przykład dotyczy szkodników rolniczych. Roślinożercy są zawsze potencjalnie poważnymi problemami dla roślin. W przypadku gdy rośliny narażone na takie ogniska mają charakter rolniczy, czyli uprawy, straty mogą być bardzo znaczące zarówno dla rolnika, jak i konsumenta. Dlatego zawsze istnieje presja, aby zapobiec takim wybuchom., Od II wojny światowej główną bronią w walce z takimi szkodnikami były pestycydy chemiczne, takie jak DDT. Jednak w ostatnich latach zdaliśmy sobie sprawę, że pestycydy te są niezwykle niebezpieczne na dłuższą metę, zarówno dla środowiska, jak i dla ludzi. W związku z tym nastąpił ruch mający na celu ograniczenie ilości pestycydów rozpylanych w celu zwalczania szkodników. Głównym sposobem jest ustalenie progu Ekonomicznego, którym jest gęstość zaludnienia potencjalnego szkodnika, poniżej której szkody w uprawie są nieznaczne(tzn. nie jest naprawdę konieczne opryskiwanie)., Gdy populacja szkodników wzrośnie powyżej tego progu, rolnik musi podjąć działania i zastosować jakiś rodzaj pestycydów lub inne środki zwalczania szkodników. Biorąc pod uwagę charakter tego problemu, czasami niezwykle ważne jest, aby móc przewidzieć, kiedy szkodnik osiągnie próg ekonomiczny. Znajomość R dla gatunków szkodników pozwala rolnikowi przewidzieć, kiedy konieczne będzie zastosowanie jakiejś procedury kontroli (rys. 3).
równanie wykładnicze jest również użytecznym modelem do rozwijania intuicyjnych pomysłów na temat populacji., Klasycznym przykładem jest staw z populacją lilii. Jeśli każda podkładka z lilii powtarza się co miesiąc (dwie podkładki zajmują miejsce, gdzie była jedna) i zajęło, powiedzmy, trzy lata, aby staw stał się w połowie wypełniony podkładkami z lilii, ile jeszcze potrwa, aby staw był całkowicie pokryty podkładkami z lilii? Jeśli nie przestaniesz myśleć zbyt jasno, kuszące jest stwierdzenie, że zajmie to tyle samo czasu, trzy lata, zanim druga połowa stawu stanie się tak wypełniona, jak pierwsza. Odpowiedź, oczywiście, jest jeden miesiąc.,
Innym popularnym przykładem jest przysłowiowy starożytny egipski (a czasem perski) matematyk, który prosi króla o zapłatę w postaci ziaren pszenicy (czasem ryżu). Jedno ziarno na pierwszym kwadracie szachownicy, dwa ziarna na drugim kwadracie i tak dalej, aż do ostatniego kwadratu. Faraon nie wyobraża sobie, że taka prosta zapłata może wynieść wiele i tak się zgadza. Nie doceniał jednak w pełni wykładniczego wzrostu., Ponieważ na szachownicy są 64 pola, możemy użyć równania 2, aby określić, ile ziaren pszenicy będzie trzeba zapłacić na ostatnim polu (r podniesiony do potęgi 64, czyli około 18 446 744 074 000 000 000-dużo pszenicy, z pewnością więcej niż w całym królestwie). Przykłady te podkreślają często zaskakujący sposób, w jaki proces wykładniczy może prowadzić do bardzo dużych liczb bardzo szybko.
