Szybka odpowiedź:
dla trójkąta prostokątnego:

funkcja sinusoidalna sin przyjmuje kąt θ i daje stosunek przeciwnej przeciwprostokątnej
odwrotna funkcja sinusoidalna Sin-1 przyjmuje stosunek przeciwnej przeciwprostokątnej i daje kąt θ
a cosinus i styczna podążają za podobną ideą.,
a teraz szczegóły:
Sinus, Cosinus i tangens są oparte na trójkącie prostokątnym
są bardzo podobnymi funkcjami … więc przyjrzymy się funkcji sinus, a następnie odwróć Sinus, aby dowiedzieć się, o co w tym wszystkim chodzi.,
funkcja sinusa
sinus kąta θ wynosi:
- długość boku przeciwległego kąta θ
- podzielona przez długość przeciwprostokątnej
lub prościej:
sin(θ) = przeciwstawna / przeciwprostokątna
funkcja sinus może nam pomóc rozwiązać takie rzeczy:
odwrotna funkcja sinus
ale czasami jest to kąt, który musimy znaleźć.
tutaj pojawia się „odwrotna sinusoida”.
odpowiada na pytanie „jaki kąt ma sinus równy przeciwnej/przeciwprostokątnej?,”
symbolem odwrotnej sinusoidy jest sin-1, a czasem arcsin.
są jak do przodu i do tyłu!

- sin przyjmuje kąt i daje nam stosunek „przeciwnej/przeciwprostokątnej”
- sin-1 przyjmuje stosunek „przeciwnej / przeciwprostokątnej” i daje nam kąt.
przykład:
Kalkulator
 |
na kalkulatorze Naciśnij jeden z następujących (w zależności od marki kalkulatora):albo '2ndf sin' lub 'shift sin'. |
na kalkulatorze spróbuj użyć sin, a następnie sin-1, aby zobaczyć, co się dzieje
więcej niż jeden kąt!
odwrotna sinusoida pokazuje tylko jeden kąt … ale jest więcej kątów, które mogą zadziałać.
przykład: oto dwa kąty, gdzie przeciwne/przeciwprostokątna = 0.,5
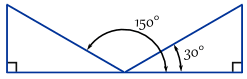
w rzeczywistości jest nieskończenie wiele kątów, ponieważ możesz dodawać (lub odejmować) 360°:
pamiętaj o tym, ponieważ są chwile, kiedy rzeczywiście potrzebujesz jednego z innych kątów!
podsumowanie
sinus kąta θ wynosi:
sin(θ) = przeciwna / przeciwprostokątna
a Sinus Odwrotny to :
sin-1 (przeciwna / przeciwprostokątna) = θ
a co z „cos” I „TAN” … ?
dokładnie ten sam pomysł, ale różne proporcje stron.,
Cosinus
cos(θ) = adjacent/Hypotenuse
i cosinus Odwrotny to:
cos-1 (Adjacent/Hypotenuse) = θ
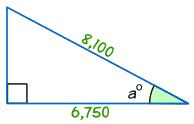
przykład: znajdź rozmiar kąta a°
cos a° = adjacent/hypotenuse
cos a° = 6,750/8,100 = 0.8333…
a° = cos-1 (0.8333…) = 33.,6° (do 1 miejsca po przecinku)
tangens
tangens kąta θ wynosi:
tan(θ) = przeciwny / sąsiadujący
więc tangens Odwrotny to :
tan-1 (opposite / adjacent) = θ
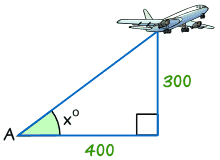
przykład: znajdź rozmiar kąta x°
tan x° = opposite / adjacent
Tan X° = 300/400 = 0.75
x° = tan-1 (0,75) = 36.,9° (poprawne do 1 miejsca po przecinku)
Inne nazwy
czasami sin-1 nazywa się asin lub arcsin
podobnie cos-1 nazywa się acos lub arccos
I TAN-1 nazywa się atan lub arctan
przykłady:
- arcsin(y) jest taki sam jak sin-1(y)
- atan(θ) jest taki sam jak tan-1(θ)
- itd.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- ale odwrotne sinusoidy i cosinusy nie ” idą w nieskończoność „jak sinusoidy i cosinusy…
spójrzmy na przykład cosinusa.
Oto cosinus i cosinus Odwrotny wykreślone na tym samym wykresie:
cosinus i cosinus Odwrotny
są to lustrzane obrazy (o przekątnej)
Ale dlaczego Cosinus Odwrotny jest odcinany na górze i na dole (kropki nie są tak naprawdę częścią funkcji) … ?
ponieważ funkcja może dać tylko jedną odpowiedź
gdy zapytamy „co to jest cos-1(x) ?,”
jedna odpowiedź lub nieskończenie wiele odpowiedzi
ale widzieliśmy wcześniej, że odpowiedzi jest nieskończenie wiele, a linia przerywana na wykresie to pokazuje.
Tak więc odpowiedzi jest nieskończenie wiele …
… ale wyobraź sobie, że wpisujesz 0.5 do kalkulatora, naciśnij cos-1 i daje Ci niekończącą się listę możliwych odpowiedzi …
mamy więc zasadę, że funkcja może dać tylko jedną odpowiedź.
tak więc, odcinając go w ten sposób otrzymujemy tylko jedną odpowiedź, ale pamiętajmy, że mogą być inne odpowiedzi.,
tangens i tangens Odwrotny
i tu jest funkcja tangens i tangens odwrotny. Czy można zobaczyć, jak są one odbicia lustrzane (o przekątnej)…?

tangens

tangens Odwrotny



