Po zbudowaniu modelu uczenia maszynowego następnym krokiem jest Ocena wydajności modelu i zrozumienie, jak dobry Jest Nasz model w stosunku do modelu benchmarkowego., Metryka oceny, które mają być używane zależy od rodzaju problemu próbujesz rozwiązać —czy jest to nadzorowany lub nienadzorowany problem, i czy jest to klasyfikacja lub regresji zadania.
w tym poście opowiem o dwóch ważnych metrykach oceny stosowanych w problemach regresji i podkreślę kluczową różnicę między nimi.
R-kwadrat, znany również jako wyznaczanie współczynnika, określa stopień, w jakim wariancja zmiennej zależnej (lub docelowej) może być wyjaśniona przez zmienną niezależną (cechy).,
zrozummy to na przykładzie — powiedzmy, że wartość R-kwadratu dla konkretnego modelu wynosi 0.7. Oznacza to, że 70% zmienności zmiennej zależnej jest wyjaśnione przez zmienne niezależne.
najlepiej byłoby, gdyby zmienne niezależne były w stanie wyjaśnić wszystkie zmiany w zmiennej docelowej. W tym scenariuszu wartość R do kwadratu wynosiłaby 1. W ten sposób możemy powiedzieć, że wyższa wartość R-kwadrat, lepiej w modelu.,
tak więc, w prostych słowach, im wyższy R do kwadratu, tym większa zmienność jest wyjaśniona przez zmienne wejściowe, a zatem lepszy jest twój model. Również R-kwadrat będzie mieścić się w zakresie od 0 do 1. Oto wzór na obliczenie R-kwadrat –
R-kwadrat jest obliczany przez podzielenie sumy kwadratów pozostałości z modelu regresji (podanego przez Ssre) przez całkowitą sumę kwadratów błędów z modelu średniego (podanego przez SStot), a następnie odjąć go od 1.,
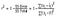
jedną z wad R-Squared jest to, że zakłada, że każda zmienna pomaga w wyjaśnieniu zmienności w celu, co może nie zawsze być prawdą. Na przykład, jeśli dodamy do danych nowe funkcje (które mogą lub nie mogą być użyteczne), wartość R-kwadratowa dla modelu wzrośnie lub pozostanie taka sama, ale nigdy nie zmniejszy się.
zajmuje się tym nieco zmodyfikowana wersja R-squared, zwana skorygowanym R-squared.,
Adjusted R-squared
podobnie jak R-squared, Adjusted R-squared mierzy zmienność zmiennej zależnej (lub docelowej), wyjaśniając tylko cechy, które są pomocne w przewidywaniu. W przeciwieństwie do R-squared, skorygowany R-squared ukarałby cię za dodanie funkcji, które nie są przydatne do przewidywania celu.
pozwól nam matematycznie zrozumieć, w jaki sposób ta funkcja jest uwzględniona w skorygowanym R-kwadracie., Oto wzór dla skorygowanego r-kwadratu

tutaj R^2 to R-kwadrat obliczony, n to liczba wierszy, A M to liczba kolumn. Wraz ze wzrostem liczby funkcji, wartość w mianowniku maleje.
- Jeśli R2 wzrośnie o znaczącą wartość, wtedy skorygowany R-kwadrat wzrośnie.
- Jeśli nie ma znaczącej zmiany w R2, wtedy skorygowany r2 zmniejszy się.
