Sekwencje geometryczne i sumy

Sekwencja

sekwencja jest zbiorem rzeczy (zwykle liczb), które są w porządku.

ciągi geometryczne

w ciągu geometrycznym każdy termin znajduje się mnożąc poprzedni termin przez stałą.

ogólnie piszemy taki ciąg geometryczny:

{a, ar, ar2, ar3,…, }

gdzie:

a jest pierwszym terminem, a
R jest czynnikiem pomiędzy terminami (zwanym „współczynnikiem wspólnym”)

ale uważaj, r nie powinno być 0:

gdy r=0, otrzymujemy sekwencję {a,0,0,…

reguła

możemy również obliczyć dowolny termin za pomocą reguły:

xn = ar(n-1)

(używamy „n-1”, ponieważ ar0 jest dla pierwszego terminu)

ciąg geometryczny może mieć również mniejsze i mniejsze wartości:

przykład:

4, 2, 1, 0.5, 0.25, …,

sekwencja ta ma współczynnik 0,5 (połowa) pomiędzy każdą liczbą.

jego reguła to xn = 4 × (0.5)n-1

dlaczego ciąg „geometryczny”?,

ponieważ to jest jak zwiększenie wymiarów w geometrii:

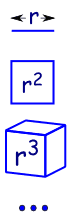	linia jest jednowymiarowa i ma długość r
	w 2 wymiarach kwadrat ma powierzchnię R2
	w 3 wymiarach kostka ma objętość R3
	itd.matematyka).,

sekwencje geometryczne są czasami nazywane Progresjami geometrycznymi (GP)

sumując szereg geometryczny

aby zsumować te:

a + ar + ar2 + … + ar(n-1)

(każdy termin to ark, gdzie k zaczyna się od 0 i przechodzi do n-1)

możemy użyć tego poręcznego wzoru:

a to pierwszy termin
r to „wspólny stosunek” między terminami
n to Liczba terminów

Co to za zabawny symbol Σ?, Jest to zapis Sigma

(zwany Sigma) oznacza „sumowanie”

i poniżej i powyżej są pokazane początkowe i wartości końcowe:

mówi „Sumuj n, gdzie n przechodzi z 1 do 4. Odpowiedź=10

formuła jest łatwa w użyciu …, po prostu „podłącz” wartości a, r I n

używając Formuły

zobaczmy formułę w akcji:

przykład: ziarna ryżu na szachownicy

na stronie cyfry binarne podajemy przykład ziarna ryżu na szachownicy. Pytanie jest zadawane:

kiedy kładziemy ryż na szachownicy:

1 ziarno na pierwszym kwadracie,
2 ziarna na drugim kwadracie,
4 ziarna na trzecim i tak dalej,
…

… podwojenie ziaren ryżu na każdym placu …

…, ile w sumie ziaren ryżu?

mamy więc:

a = 1 (Pierwszy termin)
r = 2 (podwaja się za każdym razem)
n = 64 (64 kwadraty na szachownicy)

tak:

staje się:

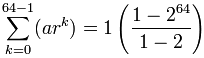
= 1-264-1 = 264 − 1

= 18,446,744,073,709,551,615

co było dokładnie wynikiem, który otrzymaliśmy na stronie cyfr binarnych (dzięki Bogu!)

i kolejny przykład, tym razem z r Mniej niż 1:

dlaczego formuła działa?,

zobaczmy, dlaczego formuła działa, bo mamy do czynienia z ciekawym „trickiem”, który warto znać.

najpierw wywołaj całą sumę „S”: S = A + ar + ar2+… + ar(n−2) + ar(n−1)

następnie należy pomnożyć S przez r: S·r = ar + ar2 + ar3+… + ar(n−1) + arn

zauważ, że S I S·R są podobne?

teraz je odjmij!

Wow! Wszystkie warunki w środku starannie anulować.,
(co jest zgrabną sztuczką)

odejmując S·R od S otrzymujemy prosty wynik:

s − S·R = A − arn

przestawimy go, aby znaleźć S:

Współczynnik S I a:S(1−R) = A(1−rn)

Podziel przez (1−R):S = A(1−RN)(1−R)

czyli nasz wzór (ta-da!):

nieskończone szeregi geometryczne

więc co się dzieje, gdy n przechodzi w nieskończoność?,

możemy użyć tej formuły:

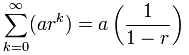
ale uważaj:

r musi być pomiędzy (ale nie wliczając) -1 i 1

i r nie powinno być 0,ponieważ Sekwencja {a,0, 0,…} nie jest geometryczny

więc nasz szereg geometryczny infnite ma skończoną sumę, gdy stosunek jest mniejszy niż 1 (i większy niż -1)

wróćmy do naszego poprzedniego przykładu i zobaczmy, co się stanie:

Nie wierzysz mi? Wystarczy spojrzeć na ten kwadrat:

dodając 12 + 14 + 18 + …

skończymy z tym wszystkim!,

powtarzające się dziesiętne

na innej stronie zapytaliśmy „robi 0.999… równe 1?”, cóż, zobaczmy, czy możemy to obliczyć: