współczynnik korelacji
Jak dobrze twoje równanie regresji naprawdę reprezentuje
Twój zbiór danych?
jednym ze sposobów ustalenia odpowiedzi na to pytanie jest zbadanie
współczynnika korelacji i współczynnika determinacji.,
|
|
współczynnik korelacji, r I |
oprócz pojawienia się informacji o regresji, wartości rand r 2 można znaleźć pod wartościami, #5 statystyki → EQ #7 R i #8 R 2 .,
współczynnik korelacji, r:
![]() ilość r, zwana współczynnikiem korelacji liniowej, mierzy siłę i
ilość r, zwana współczynnikiem korelacji liniowej, mierzy siłę i
kierunek liniowej zależności między dwiema zmiennymi. Współczynnik korelacji liniowej
jest czasami określany jako współczynnik korelacji momentu Pearsona w
na cześć jego twórcy Karla Pearsona.![]() wzór matematyczny do obliczeń wynosi:
wzór matematyczny do obliczeń wynosi: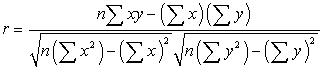
gdzie n to liczba par danych.,
(nie cieszysz się, że masz kalkulator graficzny, który oblicza tę formułę?)
![]() wartość r jest taka, że -1< r< +1. Znaki + i – są używane odpowiednio dla dodatnich
wartość r jest taka, że -1< r< +1. Znaki + i – są używane odpowiednio dla dodatnich
korelacji liniowych i ujemnych korelacji liniowych. ![]() korelacja dodatnia: Jeśli X i y mają silną dodatnią korelację liniową, R jest bliskie
korelacja dodatnia: Jeśli X i y mają silną dodatnią korelację liniową, R jest bliskie
+1. Wartość r równa dokładnie +1 oznacza idealne dopasowanie dodatnie., Wartości dodatnie
wskazują na zależność między zmiennymi x i y, tak że jak wartości dla X wzrasta,
wartości dla y również wzrastają. ![]() korelacja ujemna: jeśli X i y mają silną ujemną korelację liniową, R jest bliskie
korelacja ujemna: jeśli X i y mają silną ujemną korelację liniową, R jest bliskie
do -1. Wartość r równa dokładnie -1 oznacza idealne dopasowanie ujemne. Wartości ujemne
wskazują na zależność między x I y, taką, że jako wartości dla wzrostu x, wartości
dla zmniejszenia y. ![]() brak korelacji: jeśli nie ma korelacji liniowej lub słabej korelacji liniowej, r jest
brak korelacji: jeśli nie ma korelacji liniowej lub słabej korelacji liniowej, r jest
bliskie 0., Wartość bliska zeru oznacza, że istnieje losowa, nieliniowa relacja
między dwiema zmiennymi![]() zauważ, że r jest wielkością bezwymiarową; to znaczy, że nie zależy od jednostek
zauważ, że r jest wielkością bezwymiarową; to znaczy, że nie zależy od jednostek
.
![]() doskonała korelacja ± 1 występuje tylko wtedy, gdy wszystkie punkty danych leżą dokładnie na prostej
doskonała korelacja ± 1 występuje tylko wtedy, gdy wszystkie punkty danych leżą dokładnie na prostej
. Jeśli r = +1, nachylenie tej linii jest dodatnie. Jeżeli r= -1, nachylenie tej linii
jest ujemne. ![]() korelacja większa niż 0,8 jest ogólnie opisana jako silna, natomiast korelacja
korelacja większa niż 0,8 jest ogólnie opisana jako silna, natomiast korelacja
mniejsza niż 0.,5 jest ogólnie określana jako Wartości te mogą się różnić w zależności od”typu” badanych danych. Badanie wykorzystujące dane naukowe może wymagać silniejszej korelacji
niż badanie wykorzystujące dane z nauk społecznych.
współczynnik determinacji, r 2 lub R2:
![]() współczynnik determinacji, r 2,jest przydatny, ponieważ daje proporcję
współczynnik determinacji, r 2,jest przydatny, ponieważ daje proporcję
wariancji (fluktuacji) jednej zmiennej, która jest przewidywalna od drugiej zmiennej.,
jest to miara, która pozwala nam określić, jak pewne można być w tworzeniu
prognoz na podstawie określonego modelu/wykresu.![]() współczynnik determinacji jest stosunkiem objaśnionej zmienności do całkowitej zmienności
współczynnik determinacji jest stosunkiem objaśnionej zmienności do całkowitej zmienności
.![]() współczynnik determinacji jest taki, że 0< r 2< 1 i oznacza siłę
współczynnik determinacji jest taki, że 0< r 2< 1 i oznacza siłę
związku liniowego między x I y., ![]() współczynnik determinacji reprezentuje procent danych, który jest najbliższy
współczynnik determinacji reprezentuje procent danych, który jest najbliższy
do linii najlepszego dopasowania. Na przykład, jeśli r = 0,922, to r 2 = 0,850, co oznacza, że
85% całkowitej zmienności iny można wyjaśnić relacją liniową między x
a y (opisaną równaniem regresji). Pozostałe 15% całkowitej zmienności
W y pozostaje niewyjaśnione.![]() współczynnik determinacji jest miarą tego, jak dobrze linia regresji
współczynnik determinacji jest miarą tego, jak dobrze linia regresji
reprezentuje dane., Jeśli linia regresji przechodzi dokładnie przez każdy punkt na wykresie punktowym
, byłby w stanie wyjaśnić wszystkie zmiany. Im dalej linia jest
od punktów, tym mniej jest w stanie wyjaśnić.

