
w tym artykule dowiesz się o SVM lub maszynie wektorowej wsparcia, która jest jednym z najpopularniejszych algorytmów AI (jest to jeden z 10 najlepszych algorytmów AI) oraz o sztuczce jądra, która zajmuje się nieliniowością i wyższymi wymiarami., Poruszymy tematy takie jak hiperplany, mnożniki Lagrange ' a, będziemy mieli przykłady wizualne i przykłady kodu (podobne do przykładu kodu użytego w rozdziale KNN), aby lepiej zrozumieć ten bardzo ważny algorytm.
SVM Explained
Maszyna wektorowa jest nadzorowanym algorytmem uczenia się używanym głównie do klasyfikacji, ale może być używana również do regresji. Główną ideą jest to, że na podstawie oznaczonych danych (danych treningowych) algorytm stara się znaleźć optymalną hiperplanę, która może być używana do klasyfikacji nowych punktów danych. W dwóch wymiarach hyperplane jest prostą linią.,
Zwykle algorytm uczenia się próbuje poznać najczęstsze cechy (co odróżnia jedną klasę od drugiej) klasy i klasyfikacja opiera się na tych reprezentatywnych cechach poznanych (więc klasyfikacja opiera się na różnicach między klasami). Maszyna SVM działa na odwrót. Znajduje najbardziej podobne przykłady między klasami. To będą wektory wsparcia.
jako przykład rozważmy dwie klasy, jabłka i cytryny.,
inne algorytmy poznają najbardziej widoczne, najbardziej reprezentatywne cechy jabłek i cytryn, jak jabłka są zielone i zaokrąglone, podczas gdy cytryny są żółte i mają kształt eliptyczny.
natomiast SVM wyszukuje jabłka, które są bardzo podobne do cytryn, na przykład jabłka, które są żółte i mają kształt eliptyczny. To będzie wektor wsparcia. Drugim wektorem wsparcia będzie cytryna podobna do jabłka (zielona i zaokrąglona). Tak więc inne algorytmy uczą się różnic, podczas gdy SVM uczy się podobieństw.,
Jeśli wizualizujemy powyższy przykład w 2D, będziemy mieć coś takiego:

gdy przechodzimy od lewej do prawej, wszystkie przykłady będą klasyfikowane jako jabłka, dopóki nie osiągniemy żółtego jabłka. Od tego momentu pewność, że nowym przykładem jest jabłko, spada, podczas gdy zaufanie klasy cytryny wzrasta., Kiedy zaufanie do klasy cytrynowej staje się większe niż zaufanie do klasy jabłek, nowe przykłady będą klasyfikowane jako cytryny (gdzieś pomiędzy żółtym jabłkiem a zieloną cytryną).
bazując na tych wektorach, algorytm stara się znaleźć najlepszą hiperplanę, która oddziela klasy. W 2D hiperplane jest linią, więc wygląda to tak:

ok, ale dlaczego narysowałem niebieską granicę jak na powyższym zdjęciu?, Mogę również narysować granice w ten sposób:

jak widać, mamy nieskończoną liczbę możliwości narysowania granicy decyzji. Jak więc znaleźć optymalny?
znalezienie optymalnej Hiperplany
intuicyjnie najlepszą linią jest linia, która jest daleko od przykładów jabłkowych i cytrynowych (ma największy margines)., Aby mieć optymalne rozwiązanie, musimy zmaksymalizować marżę w obie strony (jeśli mamy wiele klas, to musimy ją zmaksymalizować biorąc pod uwagę każdą z klas).

więc jeśli porównamy obraz powyżej z obrazem poniżej, możemy łatwo zaobserwować, że pierwszy jest optymalną hiperplaną (linią), a drugi jest rozwiązaniem nieoptymalnym, ponieważ margines jest znacznie krótszy.,

ponieważ chcemy zmaksymalizować marże biorąc pod uwagę wszystkie klasy, zamiast używać jednego marginesu dla każdej klasy, używamy marginesu „globalnego”, który bierze pod uwagę wszystkie klasy., Ten margines będzie wyglądał jak fioletowa linia na poniższym obrazku:

div>
ten margines jest ortogonalny do granicy i w równej odległości do wektorów nośnych.
to gdzie mamy wektory? Każdy z obliczeń (Oblicz odległość i optymalne hiperplanaty) jest wykonywany w przestrzeni wektorowej, więc każdy punkt danych jest uważany za wektor. Wymiar przestrzeni jest określony przez liczbę atrybutów przykładów., Aby zrozumieć matematykę za, proszę przeczytać ten krótki opis matematyczny wektorów, hiperplanes i optymalizacji: SVM zwięźle.
Ogólnie rzecz biorąc, wektory nośne są punktami danych, które określają położenie i margines hiperplany. Nazywamy je wektorami „wspierającymi”, ponieważ są to reprezentatywne punkty danych klas, jeśli przesuniemy jedną z nich, zmieni się pozycja i / lub margines. Przesunięcie innych punktów danych nie będzie miało wpływu na margines lub położenie hiperplany.,
aby dokonać klasyfikacji, nie potrzebujemy wszystkich punktów danych treningowych( jak w przypadku KNN), musimy zapisać tylko Wektory podporowe. W najgorszym przypadku wszystkie punkty będą wektorami wsparcia, ale jest to bardzo rzadkie i jeśli tak się stanie, powinieneś sprawdzić swój model pod kątem błędów lub błędów.
więc zasadniczo nauka jest równoznaczna ze znalezieniem hiperplany z najlepszym marginesem, więc jest to prosty problem optymalizacji.,/h2>
podstawowe kroki SVM to:
- wybierz dwie hiperplanes (w 2D), które rozdziela dane bez punktów między nimi (czerwone linie)
- zmaksymalizuj ich odległość (margines)
- średnia linia (tutaj linia w połowie drogi między dwoma czerwonymi liniami) będzie granicą decyzji
jest to bardzo miłe i łatwe, ale znalezienie najlepszego marginesu, problem optymalizacji nie jest trywialny (łatwo jest w 2D, gdy mamy tylko dwa atrybuty, ale co jeśli mamy n wymiarów z n bardzo dużą liczbą)
aby rozwiązać problem optymalizacji, używamy mnożników Lagrange ' a., Aby zrozumieć tę technikę można przeczytać następujące dwa artykuły: dualność mnożnika Langrange 'A oraz proste wyjaśnienie, dlaczego mnożniki Langrange' a działają.
do tej pory mieliśmy dane liniowo rozdzielalne, więc mogliśmy używać linii jako granicy klasy. Ale co jeśli mamy do czynienia z nieliniowymi zbiorami danych?,
SVM dla nieliniowych zestawów danych
przykład danych nieliniowych to:

w tym przypadku nie możemy znaleźć prostej linii oddzielającej jabłka od cytryn. Więc jak możemy rozwiązać ten problem. Użyjemy sztuczki z jądrem!
podstawową ideą jest to, że gdy zbiór danych jest nierozłączny w bieżących wymiarach, Dodaj inny wymiar, być może w ten sposób dane będą rozdzielne., Pomyśl o tym, powyższy przykład jest w 2D i jest nierozłączny, ale może w 3D jest przerwa między jabłkami i cytrynami, może jest różnica poziomów, więc cytryny są na poziomie pierwszym, a cytryny na poziomie drugim. W tym przypadku możemy łatwo narysować hiperplanę rozdzielającą (w 3D hiperplanę jest płaszczyzną) między poziomem 1 A 2.
mapowanie do wyższych wymiarów
aby rozwiązać ten problem nie powinniśmy po prostu ślepo dodawać kolejnego wymiaru, powinniśmy przekształcić przestrzeń, aby celowo wygenerować tę różnicę poziomów.,
odwzorowanie z 2D na 3D
Załóżmy, że dodajemy kolejny wymiar o nazwie X3. Inną ważną transformacją jest to, że w nowym wymiarze punkty są zorganizowane za pomocą tego wzoru x12 + x22.
Jeśli wykreślimy płaszczyznę zdefiniowaną wzorem x2 + y2, otrzymamy coś takiego:

teraz musimy mapować jabłka i cytryny (które są tylko prostymi punktami) do tej nowej przestrzeni. Pomyśl o tym uważnie, co zrobiliśmy?, Użyliśmy właśnie transformacji, w której dodaliśmy poziomy oparte na odległości. Jeśli jesteś w origin, punkty będą na najniższym poziomie. Gdy oddalamy się od początku, oznacza to, że wspinamy się na wzgórze (poruszając się od środka płaszczyzny w kierunku marginesów), więc poziom punktów będzie wyższy., Teraz, jeśli weźmiemy pod uwagę, że źródłem jest cytryna z centrum, będziemy mieć coś takiego:
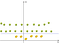
teraz możemy łatwo rozdzielić te dwie klasy. Transformacje te nazywane są jądrami. Popularne jądra to: jądro wielomianowe, jądro Gaussa, Radial Basis Function (RBF), jądro Laplace ' a RBF, jądro Sigmoidalne, jądro Anove RBF itp. (patrz funkcje jądra lub bardziej szczegółowy opis Jądra uczenia maszynowego).,
mapowanie z 1D na 2D
innym, łatwiejszym przykładem w 2D będzie:

Po użyciu jądra i po wszystkich przekształceniach otrzymamy:

tak więc po transformacji możemy łatwo rozgraniczyć dwie klasy używając tylko jednej linii.,
w rzeczywistych zastosowaniach nie będziemy mieli prostej linii prostej, ale będziemy mieli wiele krzywych i dużych wymiarów. W niektórych przypadkach nie będziemy mieć dwóch hiperplanów, które oddzielają dane bez punktów między nimi, więc potrzebujemy kompromisów, tolerancji dla wartości odstających. Na szczęście algorytm SVM ma tak zwany parametr regularyzacji, aby skonfigurować kompromis i tolerować wartości odstające.
dostrajanie parametrów
jak widzieliśmy w poprzedniej sekcji Wybór odpowiedniego jądra jest kluczowy, ponieważ jeśli transformacja jest nieprawidłowa, to model może mieć bardzo słabe wyniki., Z reguły zawsze sprawdzaj, czy masz dane liniowe i w takim przypadku zawsze używaj linear SVM (linear kernel). Linear SVM jest modelem parametrycznym, ale RBF Kernel SVM nie jest, więc złożoność tego ostatniego rośnie wraz z wielkością zestawu treningowego. Trenowanie SVM jądra RBF nie tylko jest droższe, ale także trzeba trzymać macierz jądra wokół siebie, a projekcja do tej „nieskończonej” wyższej przestrzeni wymiarowej, gdzie dane stają się liniowo rozdzielalne, jest również droższa podczas przewidywania., Co więcej, masz więcej hiperparametrów do dostrojenia, więc wybór modelu jest również droższy! I wreszcie, o wiele łatwiej jest przecenić złożony model!
Regularyzacja
parametr regularyzacji (w Pythonie nazywa się to C) mówi optymalizacji SVM, jak bardzo chcesz uniknąć pominięcia klasyfikacji każdego przykładu treningu.
Jeśli C jest wyższe, optymalizacja wybierze mniejszą hiperplane marżową, więc wskaźnik klasyfikacji danych treningowych będzie niższy.,
z drugiej strony, Jeśli C jest niskie, to marża będzie duża, nawet jeśli będą pominięte przykłady danych treningowych. Jest to pokazane na dwóch poniższych diagramach:

jak widać na obrazku, gdy c jest niskie, margines jest wyższy (więc domyślnie nie mamy tak wielu krzywych, linia nie ściśle podąża za punktami danych), nawet jeśli dwa jabłka zostały sklasyfikowane jako cytryny., Gdy C jest wysokie, granica jest pełna krzywych, a wszystkie dane treningowe zostały sklasyfikowane poprawnie. Nie zapominaj, że nawet jeśli wszystkie dane treningowe zostały poprawnie sklasyfikowane, nie oznacza to, że zwiększenie C zawsze zwiększy precyzję (z powodu nadmiernego dopasowania).
Gamma
kolejnym ważnym parametrem jest Gamma. Parametr gamma określa, jak daleko sięga wpływ pojedynczego przykładu treningowego. Oznacza to, że wysoka Gamma będzie uwzględniała tylko punkty bliskie prawdopodobnej hiperplanety, a niska Gamma będzie uwzględniała punkty znajdujące się w większej odległości.,

jak widzisz, zmniejszenie gamma spowoduje, że znalezienie właściwej hiperplany będzie uwzględniało punkty w większych odległościach, więc będzie używanych coraz więcej punktów (zielone linie wskazują, które punkty były brane pod uwagę przy znajdowaniu optymalnej hiperplany).
margines
ostatnim parametrem jest margines. Rozmawialiśmy już o marży, wyższych wynikach marży lepszy model, a więc lepsza klasyfikacja (lub przewidywanie)., Margines powinien być zawsze zmaksymalizowany.
przykład SVM używając Pythona
w tym przykładzie użyjemy Social_Networks_Ads.plik csv, ten sam plik, którego użyliśmy w poprzednim artykule, zobacz przykład użycia Pythona w KNN.
w tym przykładzie zapiszę tylko różnice między SVM i KNN, ponieważ nie chcę się powtarzać w każdym artykule! Jeśli chcesz uzyskać pełne wyjaśnienie, jak możemy odczytać zbiór danych, jak analizować i dzielić nasze dane lub jak możemy ocenić lub wykreślić granice decyzji, przeczytaj przykład kodu z poprzedniego rozdziału (KNN)!,
ponieważ biblioteka sklearn jest bardzo dobrze napisaną i przydatną biblioteką Pythona, nie mamy zbyt wiele kodu do zmiany. Jedyną różnicą jest to, że musimy zaimportować klasę SVC (SVC = SVM w sklearn) ze sklearn.svm zamiast klasy KNeighborsClassifier ze sklearn.sąsiedzi.
Po zaimportowaniu SVC możemy stworzyć nasz nowy model używając predefiniowanego konstruktora. Konstruktor ten ma wiele parametrów, ale opiszę tylko te najważniejsze, przez większość czasu nie będziesz używał innych parametrów.,
najważniejsze parametry to:
- kernel: Typ jądra, który ma być użyty. Najczęstsze jądra to RBF( jest to wartość domyślna), poly lub sigmoid, ale można również utworzyć własne jądro.,
- C: jest to parametr regularyzacji opisany w sekcji Parametry strojenia
- gamma: zostało to również opisane w sekcji Parametry strojenia
- stopień: jest używany tylko wtedy, gdy wybrane jądro jest polinomem i ustawia stopień polinoma
- prawdopodobieństwo: jest to parametr logiczny i jeśli jest to prawda, to model zwróci dla każdej prognozy wektor prawdopodobieństwa przynależności do każdej klasy zmiennej odpowiedzi. Więc w zasadzie daje pewność dla każdej prognozy.,
- kurczenie się: pokazuje, czy chcesz użyć heurystyki kurczenia w optymalizacji maszyny SVM, która jest używana w sekwencyjnej optymalizacji minimalnej. Jego domyślna wartość to true, a jeśli nie masz dobrego powodu, nie zmieniaj tej wartości na false, ponieważ kurczenie znacznie poprawi wydajność, przy bardzo niewielkiej utracie dokładności w większości przypadków.
teraz pozwala zobaczyć wynik uruchomienia tego kodu., Granica decyzyjna dla zestawu szkoleniowego wygląda następująco:

jak widzimy i jak dowiedzieliśmy się w sekcji Parametry strojenia, ponieważ c ma małą wartość (0.1) granica decyzji jest gładka.
teraz jeśli zwiększymy C z 0.,1 do 100 będziemy mieć więcej krzywych w granicy decyzji:

co by się stało, gdybyśmy użyli C=0.1, ale teraz zwiększymy gamma z 0.1 do 10? Zobaczmy!

co tu się stało? Dlaczego mamy taki zły model?, Jak zauważyliście w sekcji Parametry strojenia, wysoka gamma oznacza, że przy obliczaniu prawdopodobnej hiperplanety bierzemy pod uwagę tylko punkty, które są bliskie. Ponieważ gęstość punktów zielonych jest wysoka tylko w wybranym regionie zielonym, w tym regionie punkty są wystarczająco blisko prawdopodobnej hiperplany, więc te hiperplany zostały wybrane. Bądź ostrożny z parametrem gamma, ponieważ może to mieć bardzo zły wpływ na wyniki twojego modelu, jeśli ustawisz go na bardzo wysoką wartość (to, co jest „bardzo wysoką wartością”, zależy od gęstości punktów danych).,
dla tego przykładu najlepsze wartości dla C i Gamma to 1.0 i 1.0. Teraz, jeśli uruchomimy nasz model na zestawie testowym, otrzymamy następujący schemat:

i macierz zamieszania wygląda tak:

jak widzisz, mamy tylko 3 fałszywe pozytywy i tylko 4 fałszywe negatywy., Dokładność tego modelu wynosi 93% co jest naprawdę dobrym wynikiem, uzyskaliśmy lepszy wynik niż przy użyciu KNN (który miał dokładność 80%).
Uwaga: dokładność nie jest jedyną metryką używaną w ML, a także nie jest najlepszą metryką do oceny modelu, ze względu na paradoks dokładności. Używamy tej metryki dla uproszczenia, ale później, w rozdziale metryki do oceny algorytmów AI porozmawiamy o paradoksie dokładności i pokażę inne bardzo popularne metryki używane w tej dziedzinie.,
wnioski
w tym artykule widzieliśmy bardzo popularny i potężny algorytm uczenia nadzorowanego, maszynę wektorową wsparcia. Poznaliśmy podstawową ideę, czym jest hiperplaneta, czym są wektory podporowe i dlaczego są tak ważne. Widzieliśmy również wiele wizualnych reprezentacji, które pomogły nam lepiej zrozumieć wszystkie pojęcia.
kolejnym ważnym tematem, który poruszyliśmy, jest sztuczka z jądrem, która pomogła nam rozwiązać nieliniowe problemy.
aby mieć lepszy model, widzieliśmy techniki dostrajania algorytmu., Na końcu artykułu mieliśmy przykład kodu w Pythonie, który pokazał nam, jak możemy używać algorytmu KNN.
jako ostatnie przemyślenia chciałbym podać kilka plusów & minusy i kilka popularnych przypadków użycia.,
plusy
- SVN może być bardzo wydajny, ponieważ wykorzystuje tylko podzbiór danych treningowych, tylko Wektory wsparcia
- działa bardzo dobrze na mniejszych zestawach danych, na nieliniowych zestawach danych i przestrzeniach o wysokich wymiarach
- jest bardzo skuteczny w przypadkach, gdy liczba wymiarów jest większa niż liczba próbek
- może mieć wysoką dokładność, czasami może wykonywać nawet lepiej niż sieci neuronowe
- nie bardzo wrażliwy na przerobienie
cons
- czas treningu jest wysoki, gdy mamy duże zbiory danych
- , gdy zbiór danych ma więcej szumów (i.,klasy docelowe nakładają się na siebie) SVM nie działa dobrze
popularne przypadki użycia
- Klasyfikacja tekstu
- wykrywanie spamu
- analiza nastrojów
- Rozpoznawanie oparte na aspekcie
- Odręczne rozpoznawanie cyfr
