Cum de creștere a populației: Exponențială și Logaritmică Ecuații

Cel mai simplu mod de a capta ideea de creștere a populației este cu un singur organism, cum ar fi o bacterie sau un cilliate. În Figura 1, este prezentată o populație de Paramecium într-un mic diapozitiv de depresie de laborator. În această populație, indivizii se împart o dată pe zi. Deci, începând cu o singură persoană în ziua 0, ne așteptăm, în zile succesive, 2, 4, 8, 16, 32, și 64 de persoane din populație., Putem vedea aici că, într-o anumită zi, numărul de indivizi din populație este pur și simplu de două ori mai mare decât numărul cu o zi înainte, deci numărul de astăzi, numiți-l N(astăzi), este egal cu dublul numărului de ieri, numiți-l n(ieri), pe care îl putem scrie mai compact ca N(astăzi) = 2N(ieri).deci, are sens să scrie acest lucru ca, N (t) = 2n(t – 1) Unde t ar putea lua orice valoare.,acum putem generaliza această idee puțin dacă observăm că în ziua a șasea numărul este egal cu dublul numărului din ziua a cincea sau N(6) = 2n(5) și în ziua a cincea numărul este egal cu dublul numărului din ziua a patra sau N(5) = 2n(4) etc.

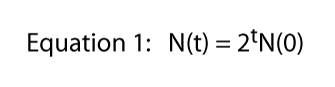
unde t reprezintă orice timp, la toate (de exemplu, dacă t = 6, N(6) = 26).în cele din urmă, observăm că această ecuație a fost derivată din situația specifică prezentată în Figura 1, unde o diviziune pe zi era regula grea și rapidă., De acolo vine 2 în ecuația 1 — din fiecare parameciu individual obținem doi indivizi a doua zi. Desigur, rata de divizare ar putea fi orice. Dacă ar exista două diviziuni pe zi, dar o celulă a murit întotdeauna, ne-am aștepta la trei indivizi de la fiecare individ și ecuația 1 ar fi N(t) = 3TN(0)., Astfel, rata de divizare a putea fi orice număr, la toate și ecuația generală devine,

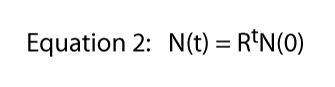
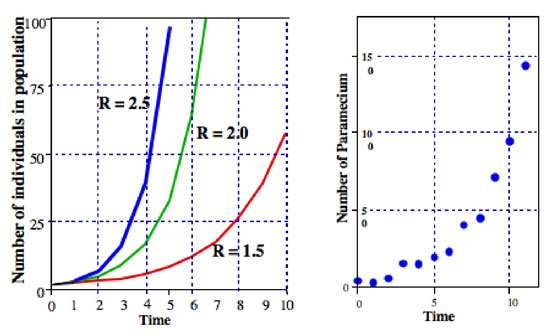
în cazul în care R este de obicei numit finite rata de creștere a populației (în caz de divizare Parameci finite rata de creștere a populației este egală cu rata de divizare). În Figura 2 ilustrăm această ecuație pentru diferite valori ale lui R. în mod normal este denumită ecuația exponențială, iar forma datelor din Figura 2 este forma generală numită exponențială.,

Figura 2: Stânga: formă generală de creștere exponențială a populației (ecuația 2). Dreapta: numere reale de Paramecium într-o probă de 1 cc dintr-o cultură de laborator.orice valoare a lui R poate fi reprezentată într-un număr infinit de moduri (de exemplu, dacă R = 16, am putea scrie R = 8 x 2 sau R = 42 sau R = 32/2 sau R = 2.718282.77). Această ultimă Expresie (R = 2.718282.,77) folosește o constantă importantă care ar putea fi amintită din calculul elementar, constanta lui Euler. Exprimarea valorii R ca constantă a lui Euler ridicată la o anumită putere este de fapt extrem de utilă — aduce întreaga putere a calculului în imagine.,olize lui Euler constantă ca e putem scrie Ecuația 2 ca

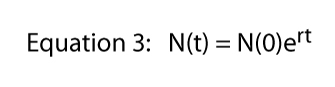
Acum, dacă ne-am lua log natural din ambele părți ale Ecuației 3 — amintiți-vă ln(ex) = x — Ecuația 3 devine: ln = ln + rt

Și dacă am început populație cu un singur individ (ca în exemplul de mai sus), avem

din care vedem că log natural din populație, la un anumit moment, este ceva constant, ori acel moment., Constanta r este denumită rata intrinsecă a creșterii naturale (Figura 2).tot felul de microorganisme prezintă modele care sunt foarte apropiate de creșterea exponențială a populației. De exemplu, în graficul din dreapta din Figura 2 este o populație de Paramecium care crește într-o cultură de laborator. Modelul de creștere este foarte apropiat de modelul ecuației exponențiale.un alt mod de a scrie ecuația exponențială este ca o ecuație diferențială, adică reprezentând creșterea populației în forma sa dinamică., Mai degrabă decât a cere ceea ce este dimensiunea populației la momentul t, ne întrebăm, ce este rata la care populația este în creștere la momentul t. Rata este simbolizat ca dN/dt, care înseamnă pur și simplu „schimbare în N raport cu schimbare în t,” și dacă vă amintiți dumneavoastră de bază de calcul, putem găsi rata de creștere prin diferențierea Ecuației 4, ceea ce ne oferă

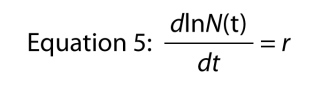
ceea ce este remarcabil, pentru că se spune că rata de creștere a jurnalului de numărul populației este constantă., Această rată constantă de creștere a jurnalului populației este rata intrinsecă de creștere.,

Amintiți-vă că rata de schimbare a jurnalului de un număr este la fel ca „pe cap de locuitor” schimbare în acest număr, ceea ce înseamnă că putem scrie Ecuația 5 ca

în cazul în care am omite variabila t, deoarece este evident unde se duce, și apoi ne-am rearanja un pic de a veni cu

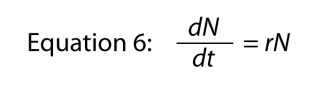
în cazul în care parametrul r este, din nou, rata intrinsecă a creșterii naturale., Relația de bază dintre rata finită de creștere și rata intrinsecă este

r = ln(R)

unde Ln se referă la logaritmul natural. Rețineți că ecuația 6 și ecuația 3 sunt doar forme diferite ale aceleiași ecuații (ecuația 3 este forma integrată a ecuației 6; ecuația 6 este forma diferențiată a ecuației 3) și ambele pot fi denumite pur și simplu ecuația exponențială.,

Figura 3: caz Ipotetic de un parazit populației într-un agroecosistem

în Conformitate cu modelul 1 (care are un număr relativ mare de estimare a R), fermierul trebuie să se gândească la aplicarea unei proceduri de control la jumătatea sezonului. Conform modelului 2 (care are o estimare relativ mică A R), fermierul nu trebuie să-și facă griji cu privire la controlul dăunătorilor, deoarece populația sa depășește pragul economic numai după recoltare., În mod clar, este important să știți ce model este corect. În acest caz, conform datelor disponibile (Puncte de date albastre), fie modelul 1, fie modelul 2 pare să se potrivească, lăsând fermierul încă în uitare.

ecuația exponențială este un model util de populații simple, cel puțin pentru perioade relativ scurte de timp., De exemplu, dacă un tehnician de laborator trebuie să știe când o cultură bacteriană ajunge la o anumită densitate a populației, exponențiale ecuația poate fi folosit pentru a oferi o predicție când exact dimensiunea populației va fi atins. Un alt exemplu este în cazul dăunătorilor agricoli. Erbivorele sunt întotdeauna probleme potențial majore pentru plante. Atunci când plantele supuse unor astfel de focare sunt agricole, adică culturi, pierderea poate fi foarte semnificativă atât pentru fermier, cât și pentru consumator. Astfel, există întotdeauna presiune pentru a preveni astfel de focare., De la al doilea război mondial arma majoră în combaterea acestor focare de dăunători a fost pesticidele chimice, cum ar fi DDT. Cu toate acestea, în ultimii ani am ajuns să ne dăm seama că aceste pesticide sunt extrem de periculoase pe termen lung, atât pentru mediu, cât și pentru oameni. În consecință, a existat o mișcare pentru a limita cantitatea de pesticide care sunt pulverizate pentru a combate dăunătorii. Principalul mod în care se face acest lucru este stabilirea unui prag economic, care este densitatea populației potențialului dăunător sub care deteriorarea culturii este nesemnificativă (adică nu este cu adevărat necesar să se pulverizeze)., Când populația de dăunători crește peste acest prag, fermierul trebuie să ia măsuri și să aplice un fel de pesticid sau alte mijloace de combatere a dăunătorilor. Având în vedere natura acestei probleme, uneori este extrem de important să se poată prezice când dăunătorul va atinge pragul economic. Cunoașterea R pentru speciile dăunătoare permite fermierului să prezică când va fi necesar să aplice un fel de procedură de control (Figura 3).

ecuația exponențială este, de asemenea, un model util pentru dezvoltarea ideilor intuitive despre populații., Exemplul clasic este un iaz cu o populație de tampoane de crin. Dacă fiecare tampon de crin se reproduce (două tampoane iau locul unde fusese un tampon) în fiecare lună și a durat, să zicem, trei ani pentru ca iazul să devină pe jumătate umplut cu tampoane de crin, cât va mai dura pentru ca iazul să fie complet acoperit cu tampoane de crin? Dacă nu vă opriți să gândiți prea clar, este tentant să spuneți că va dura la fel de mult timp, trei ani, pentru ca a doua jumătate a iazului să devină la fel de umplută ca prima. Răspunsul, desigur, este de o lună., un alt exemplu popular este proverbialul matematician egiptean antic (sau uneori persan) care solicită plata de la rege sub formă de boabe de grâu (uneori orez). Un bob pe primul pătrat al unei table de șah, două boabe pe al doilea pătrat și așa mai departe, până la ultimul pătrat. Faraonul nu-și poate imagina că o astfel de plată simplă ar putea ajunge la mult, și astfel este de acord. Dar el nu a apreciat pe deplin creșterea exponențială., Deoarece există 64 de pătrate de pe tabla de șah, putem folosi Ecuația 2 pentru a determina cât de multe boabe de grâu va fi obligat să plătească pe ultimul pătrat (R ridicat la 64 de putere, care este de aproximativ 18,446,744,074,000,000,000 — o mulțime de grâu într-adevăr, cu siguranță mai mult decât în întregul regat). Aceste exemple subliniază modul frecvent surprinzător în care un proces exponențial poate duce la un număr foarte mare foarte rapid.