Răspuns Rapid:
Pentru un triunghi dreptunghic:

sinusul funcția păcatul are unghiul θ și dă raportul opus ipotenuza
arcsinusului funcția sin-1 are raportul oppositehypotenuse și dă unghiul θ
Și cosinus și tangenta urmeze o idee similară.,
și acum pentru detalii:
sinusul, cosinusul și tangenta se bazează pe un triunghi în unghi drept
acestea sunt funcții foarte similare … deci, ne vom uita la funcția sinusoidală și apoi inversă sinusoidală pentru a afla despre ce este vorba.,
Sinus Funcția
Sinusul unghiului θ este:
- lungimea de partea Opusă unghiului θ
- împărțită la lungimea Ipotenuzei
Sau, mai simplu:
sin(θ) = Opusa / Ipotenuza
Sinusul Funcție poate ne ajuta să rezolvăm lucruri de genul asta:
arcsinusului Funcția
Dar uneori este unghiul avem nevoie pentru a găsi.
Acest lucru este în cazul în care „Inverse Sine” vine. acesta răspunde la întrebarea ” ce unghi are sinus egal cu opusul / hypotenuse?,Simbolul pentru sinusul invers este sin-1, sau uneori arcsin.
ele sunt ca înainte și înapoi!

- păcatul are un unghi și ne dă raportul „opusa/ipotenuza”
- sin-1 are raportul „opusa/ipotenuza” și ne dă unghiul.
exemplu:
Calculator
 |
Pe calculator apăsați una din următoarele (în funcție de marcă de calculator):fie ‘2ndF păcat” sau „shift păcat’. |
pe calculatorul dvs., încercați să utilizați sin și apoi sin-1 pentru a vedea ce se întâmplă
mai mult de un unghi!
sinusul invers vă arată doar un unghi … dar există mai multe unghiuri care ar putea funcționa.
exemplu: aici sunt două unghiuri unde opus / hypotenuse = 0.,5
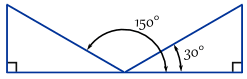
de fapt, există infinit mai multe unghiuri, pentru că puteți păstra adăugarea (sau scăderea) 360°:
Amintiți-vă acest lucru, pentru că există momente când ai nevoie de unul din alte unghiuri!
Sumar
Sinusul unghiului θ este:
sin(θ) = Opusa / Ipotenuza
Și arcsinusului este :
sin-1 (Opusa / Ipotenuza) = θ
Ce Zici de „cos” și „tan” … ?
exact aceeași idee, dar rapoarte laterale diferite.,
Cosinus
Cosinus de unghi θ este:
cos(θ) = Adiacente / Ipotenuza
Și Cosinus Inverse este :
pentru că-1 (Adiacente / Ipotenuza) = θ
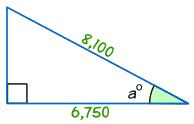
Exemplu: Găsiți dimensiunea de un unghi°
pentru o° = Adiacente / Ipotenuza
pentru o° = 6,750/8.100 de = 0.8333…
a° = cos-1 (0,8333…) = 33.,6° (la 1 zecimală)
Tangenta
Tangenta unghiului θ este:
tan(θ) = Opusa / cateta alăturată
Deci, Inversul Tangentei este :
tan-1 (Vizavi / Adiacente) = θ
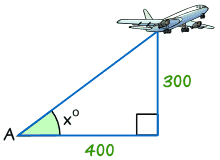
Exemplu: Găsi mărimea unghiului x°
tan x° = Opusa / cateta alăturată
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (corect la 1 zecimală)
Alte Nume
Uneori sin-1 se numește asin sau arcsin
de Asemenea, pentru că-1 se numește acos sau arccos
Si tan-1 se numește atan sau arctan
Exemple:
- arcsin(y) este la fel ca sin-1(y)
- atan(θ) este aceeași ca și tan-1(θ)
- etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- dar sinusul invers și cosinusul invers nu „continuă pentru totdeauna”, așa cum fac sinusul și cosinusul …
să ne uităm la exemplul de cosinus.
Aici este Cosinusul și Cosinus Inverse reprezentate pe același grafic:
Cosinus și Cosinus Inverse
Acestea sunt imagini în oglindă (despre diagonala)
Dar de ce nu Invers Cosinus se taie în partea de sus și de jos (punctele nu sunt chiar o parte a funcției) … ?
deoarece pentru a fi o funcție poate da doar un singur răspuns
atunci când ne întrebăm ” ce este cos-1 (x) ?,”
un răspuns sau infinit de multe răspunsuri
dar am văzut mai devreme că există infinit de multe răspunsuri, iar linia punctată din grafic arată acest lucru.deci, da, există infinit de multe răspunsuri …
… dar imaginați-vă că tastați 0.5 în calculatorul dvs., apăsați cos-1 și vă oferă o listă fără sfârșit de răspunsuri posibile … deci, avem această regulă că o funcție poate da doar un singur răspuns.deci, tăind-o astfel, obținem doar un singur răspuns, dar ar trebui să ne amintim că ar putea exista și alte răspunsuri.,
tangenta si tangenta inversa
si aici este functia tangenta si tangenta inversa. Puteți vedea cum sunt imagini în oglindă (despre diagonală) …?

Tangenta

Inverse Tangent



