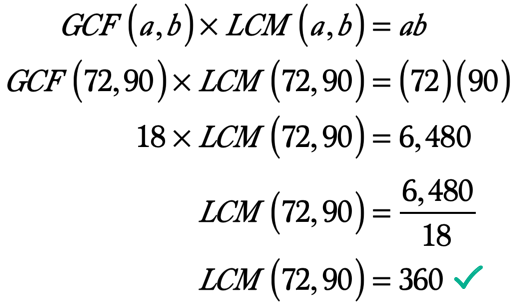când ați studiat cum să găsiți GCF și LCM a două numere pozitive, ați descoperit o relație foarte interesantă între cele două cantități?

am făcut-o! Am descoperit-o din întâmplare când eram tânăr student și am crezut că am dat peste ceva „revoluționar”. Am fost atât de entuziasmat încât am împărtășit-o cu profesorul meu., Dar spre frustrarea mea, m-a privit în ochi și mi-a spus că era deja o declarație matematică dovedită. M-am simțit descurajat pentru o clipă, dar m-am întors la școală și am continuat.

Dacă nu ați întâlnit încă, există o remarcabilă algebrice relația sau legătura dintre cel mai Mare divizor Comun (CMMDC) și cel mai mic Multiplu Comun (LCM) de două numere. În această lecție, numerele pe care le dorim sunt cele care aparțin numai setului de numere întregi pozitive.,
mai jos este legătura algebrică dintre GCF și LCM a două numere întregi pozitive.
GCF-LCM Formula
AVERTISMENT: nu Există nici un astfel de lucru ca „GCF-LCM Formula”. Tocmai am făcut numele pentru ușurința de referință. Puteți să-l numiți orice doriți, atâta timp cât își servește scopul.,
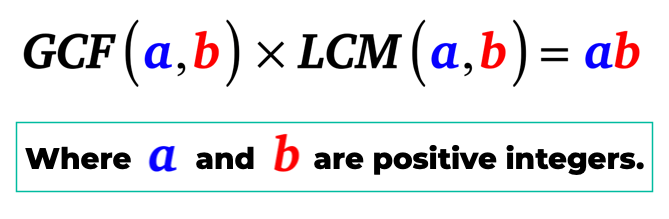
pur și Simplu pune, cel mai mare divizor comun al lui a și b atunci când este multiplicată cu cel mai mic multiplu comun dintre a și b este egală cu produsul dintre a și b. Asta este, a și b sunt numere întregi pozitive.
Exemplu Probleme
Exemplu 1: GCF de 12 și 16 este 4. Care este LCM de 12 și 16?
puteți determina LCM de 12 și 16 folosind oricare dintre cele două metode de mai jos.,
- găsirea LCM folosind metoda listei
- găsirea LCM folosind metoda factorizării Prime
cu toate acestea, există un mod mult mai rapid. Puteți profita de” Formula GCF-LCM”, deoarece cunoașteți cele două numere întregi și GCF-ul său. Doar conectați valorile în formula, apoi rezolvați pentru LCM.
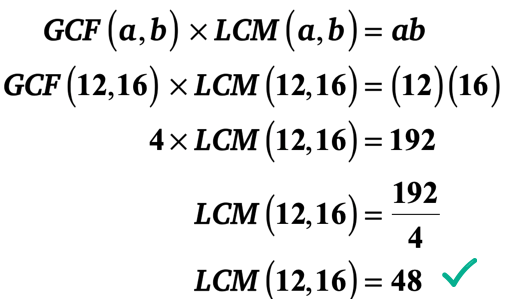
nu voi lăsa să vă pentru a verifica dacă LCM de 12 și 16 ani este, într-adevăr, 48.
Exemplul 2: LCM de 24 și 40 este 120. Care este GCF de 24 și 40?,
această problemă este exact opusul exemplului 1, deoarece vi se oferă valoarea LCM în loc de GCF.deci, acestea sunt informațiile pe care le cunoaștem. Să le enumerăm pentru claritate.▶︎ a = 24 și b=40 prin urmare ab=\left ({24} \right)\left ({40} \right) = 960
📌 Notă: Nu contează cu adevărat ce numere sunt a și b. nu va schimba rezultatul răspunsului final. Cu toate acestea, este o bună practică să vă standardizați soluția. Vă sugerez să lăsați o să fie întreg mai mic în timp ce B să fie întreg mai mare.,
să înlocuim valorile cunoscute în formula, apoi să rezolvăm pentru GCF de 24 și 40.
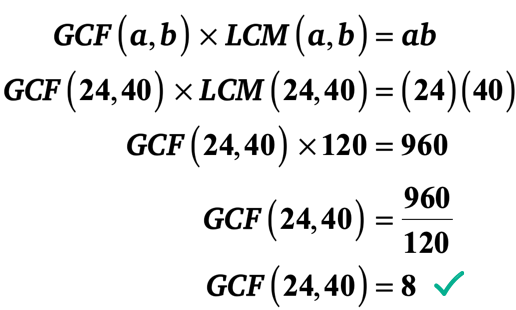
Exemplul 3: Găsiți GCF de 20 și 25 de prima calcularea LCM de 20 și 25 de ani.această problemă va fi puțin diferită de exemplele #1 și #2. Va trebui să calculați mai întâi cel mai mic multiplu comun (LCM) de 20 și 25. După aceea, puteți rezolva pentru cel mai mare Factor comun (GCF) de 20 și 25 folosind formula GCF-LCM.
deci, aici vom merge!, Pentru a găsi LCM de 20 și 25, vom scrie primele câteva multipli de 20 și 25. Primul multiplu comun care apare va fi LCM-ul nostru.
Multipli de 20: 20, 40, 60, 80, 100, 120
Multipli de 25: 25, 50, 75, 100, 125, 150
Deoarece numărul 100 apare ca primul multiplu comun al 20 și 25 de ani, atunci putem pretinde că LCM de 20 și 25 de ani este de 100.
acum avem toate informațiile pentru a utiliza formula. Mai jos sunt valorile pe care le vom înlocui în formula de rezolvat pentru LCM de 20 și 25.,
◉ produsul dintre a și b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ LCM de 20 și 25 → LCM\left( {20,25} \right) = 100
Aici e calcul pentru a rezolva pentru GCF de 20 și 25 de ani:
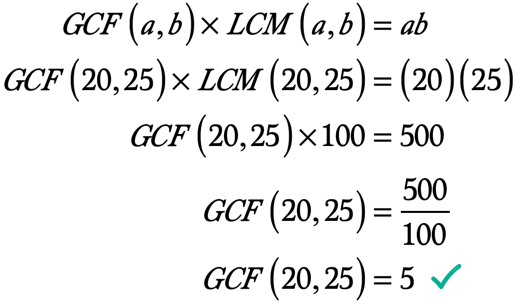
Exemplul 4: Găsiți LCM de 63 și 84 de prima calcularea CMMDC de 63 și 84.
această problemă este foarte asemănătoare cu exemplul # 3. Singura diferență este că veți calcula mai întâi GCF în loc de LCM, conform instrucțiunilor problemei în sine.,să găsim toți factorii 63 și 84. Puteți utiliza tehnica „metoda curcubeului” pentru a factor numerele întregi date.observați că cel mai mare sau cel mai mare factor comun dintre cele două liste este 21.
Factori de 63: 1, 3, 7, 9, 21, 63
Factori de 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
prin Urmare, cel mai Mare Factor Comun de 63 și 84 este de 21. Astfel, GCF \ left ({63,84} \right) = 21.,
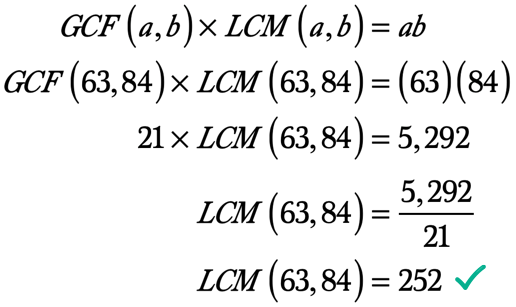
Exemplul 5: Găsiți LCM de 72 și 90 folosind GCF-LCM Formula.după cum știm deja, putem găsi LCM a două numere întregi cu valoarea GCF folosind Formula GCF-LCM.,
Listare atât factorii de 72 și 90 de ani, avem:
Toți factorii de 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Toți factorii de 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Când ne-am compara listele de factori, vom vedea că 18 este factorul care este comun pentru ambele, dar are cea mai mare sau cea mai mare în valoare. Aceasta înseamnă că GCF de 72 și 90 este 18, adică GCF \ left ({72,90} \ right) = 18.acum suntem gata să înlocuim valorile de mai jos în formulă.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Aici e calcul pentru a găsi LCM având în vedere că știm deja CMMDC a două numere întregi și produsul lor.