După construirea unui model de învățare mașină, următorul pas este de a evalua modelul de performanță și de a înțelege cât de bine modelul nostru este împotriva un model de referință., Metrica de evaluare care trebuie utilizată depinde de tipul de problemă pe care încercați să o rezolvați —indiferent dacă este o problemă supravegheată sau nesupravegheată și dacă este o clasificare sau o sarcină de regresie.în această postare voi vorbi despre două valori importante de evaluare utilizate pentru problemele de regresie și voi evidenția diferența cheie dintre ele.
R-pătrat, cunoscut și sub numele de determinarea coeficientului, definește gradul în care varianța variabilei dependente (sau țintă) poate fi explicată prin variabila independentă (caracteristici).,
să înțelegem acest lucru cu un exemplu-să spunem că valoarea R-pătrat pentru un anumit model este de 0,7. Aceasta înseamnă că 70% din variația variabilei dependente este explicată prin variabilele independente.în mod ideal, am dori ca variabilele independente să poată explica toate variațiile variabilei țintă. În acest scenariu, valoarea R-pătrat ar fi 1. Astfel, putem spune că este mai mare valoarea R-pătrat, mai bine în model.,
Deci, în termeni simpli, mai mare R pătrat, variația mai mult se explică prin variabilele de intrare și, prin urmare, mai bine este modelul. De asemenea, R-pătrat ar varia de la 0 la 1. Aici este formula de calcul R-squared-
R-squared este calculată prin împărțirea sumei pătratelor reziduurilor din modelul de regresie (oferit de SSres) cu suma totală a pătratelor erorilor de la modelul de mediu (date de SStot) și apoi se scade la 1.,
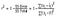
Un dezavantaj al r-pătrat este ca se presupune fiecare variabilă ajută în explicarea variației în țintă, care ar putea să nu fie întotdeauna adevărat. De exemplu, dacă adăugăm noi caracteristici datelor (care pot sau nu pot fi utile), valoarea R-pătrat pentru model ar crește sau ar rămâne aceeași, dar nu ar scădea niciodată.aceasta este îngrijită de o versiune ușor modificată a R-pătrat, numită R-pătrat ajustat.,
ajustat R-pătrat
Similar cu R-pătrat, ajustat R-pătrat măsoară variația variabilei dependente (sau țintă), explicată doar prin caracteristicile care sunt utile în a face predicții. Spre deosebire de R-pătrat, R-pătrat ajustat vă va penaliza pentru adăugarea de caracteristici care nu sunt utile pentru prezicerea țintei.
să înțelegem matematic modul în care această caracteristică este cazată în R-pătrat ajustat., Aici este formula pentru adjusted r-squared

Aici R^2 este r-pătrat calculată, N este numărul de rânduri și M este numărul de coloane. Pe măsură ce numărul de caracteristici crește, valoarea numitorului scade.
- dacă R2 crește cu o valoare semnificativă, atunci R-pătrat ajustat ar crește.
- dacă nu există o schimbare semnificativă în R2, atunci R2 ajustat ar scădea.
