secvență
o secvență este un set de lucruri (de obicei numere) care sunt în ordine.
secvențe geometrice
într-o secvență geometrică fiecare termen se găsește prin înmulțirea termenului anterior cu o constantă.
în general, scriem o secvență geometrică astfel:
{a, ar, ar2, AR3, …, }
unde:
- a este primul termen și
- r este factorul dintre termeni (numit „raportul comun”)
dar fii atent, r nu ar trebui să fie 0:
- când r=0, obținem secvența {a,0,0,…} care nu este geometrice
Regula
putem calcula, de asemenea, orice termen, folosind Regula:
xn = ar(n-1)
(Vom folosi „n-1” pentru că ar0 este pentru termenul de 1)
O progresie Geometrică poate avea, de asemenea, mai mici și mai mici valori:
Exemplu:
4, 2, 1, 0.5, 0.25, …, această secvență are un factor de 0,5 (jumătate) între fiecare număr.
regula sa este xn = 4 × (0,5)n-1
De ce secvența” geometrică”?,
Pentru că este ca și cum crește dimensiuni în geometrie:
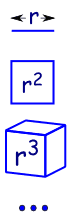 |
o linie este 1-dimensional și are o lungime de r |
| în 2 dimensiuni-un pătrat are o suprafata de r2 | |
| în 3 dimensiuni-un cub are volumul r3 | |
| etc (da, putem avea 4 și mai multe dimensiuni în matematică)., |
Secvențe Geometrice sunt uneori numite Progresii Geometrice (G. P. s)
Însumând o Serie Geometrică
Pentru suma acestea:
un + ar + ar2 + … + ar(n-1)
(Fiecare termen este arca, unde k incepe de la 0 și urcă până la n-1)
putem folosi acest lucru la îndemână formula:

a este primul termen
r este comun „raport” între termenii
n este numărul de termeni
Ce este așa de amuzant Σ simbol?, Este numit Sigma Notația
| (numit Sigma) înseamnă „rezuma” |
Și mai jos și mai sus, sunt prezentate începând și terminând valori:
Se spune „Rezuma n, unde n se duce de la 1 la 4. Răspuns=10
formula este ușor de utilizat …, doar „plug-in” valorile a, r și n,
Folosind Formula
Să vedem formula în acțiune:
Exemplu: Boabe de Orez pe o Tablă de Șah

Pe pagina de Cifre Binare vom da un exemplu de boabe de orez pe o tabla de sah. Se pune întrebarea:
când așezăm orezul pe o tablă de șah:
- 1 boabe pe primul pătrat,
- 2 boabe pe al doilea pătrat,
- 4 boabe pe al treilea și așa mai departe,
- …
… dublarea boabelor de orez pe fiecare pătrat …
…, câte boabe de orez în total?
Deci, avem:
- o = 1 (primul termen)
- r = 2 (se dublează de fiecare dată)
- n = 64 (64 de pătrate de pe tabla de șah)
Astfel:

Devine:
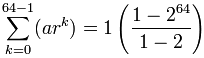
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Care a fost exact rezultatul la care am ajuns pe Cifre Binare pagina (slavă domnului!)
și un alt exemplu, de data aceasta cu r mai mic de 1:
De ce funcționează Formula?,
Să vedem de ce funcționează formula, pentru că ajungem să folosim un „truc” interesant care merită știut.
observați că S și s·r sunt similare?acum scade-le!
Wow! Toți termenii din mijloc anulează cu ușurință., prin scăderea S·r din S obținem un rezultat simplu:
S − S·r = a − arn
să−l rearanjăm pentru a găsi S:
care este formula noastră(ta-da!):

serii geometrice Infinite
deci ce se întâmplă când N merge la infinit?,
putem folosi această formulă:
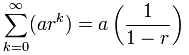
Dar fii atent:
r trebuie să fie între (dar nu inclusiv) -1 și 1
și r nu ar trebui să fie 0 pentru că secvența {a,0,0,…} nu este geometrice
Deci infnite serie geometrică are o sumă finită atunci când raportul este mai mic decât 1 (și mai mare decât -1)
Să aducem înapoi exemplul anterior, și văd ce se întâmplă.
|
nu mă crezi? Uită-te la acest pătrat: prin adăugarea 12 + 14 + 18 + … terminăm cu totul!, |
 |
Recurente Zecimal
Pe o altă pagină ne-a întrebat „Nu 0.999… Egal 1?”, Ei bine, să vedem dacă o putem calcula:



