co je tepelná roztažnost?
tepelná roztažnost je jev, kdy objekt nebo tělo expanduje v reakci na zahřátí. Tepelná roztažnost je nejzřetelnější u plynů a kapalin, ale může mít stále značný vliv na pevné látky.

1: železniční tratě ohnuté vzhledem k lineární tepelné roztažnosti
tepelné vlastnosti tuhých látek jsou velmi důležitým aspektem při návrhu továrny a produkty., Pokud se během výstavby a návrhu neuvažuje o tepelné roztažnosti, mohlo by to mít za následek velké strukturální poškození stroje nebo budovy. Bylo přijato nespočet opatření k tomu, aby se tomu zabránilo, a na základě tohoto jevu se vyvíjí mnoho důmyslných technologií. Množství, které Materiál expanduje, lze vysvětlit zvážením koeficientu odpovídajícího frakčnímu růstu materiálu na změnu stupně teploty. Tento koeficient se nazývá koeficient tepelné roztažnosti a používá se k předpovědi růstu materiálů v reakci na známou změnu teploty., Čím větší je tento koeficient pro materiál, tím více se rozšíří na zvýšení teploty stupně.
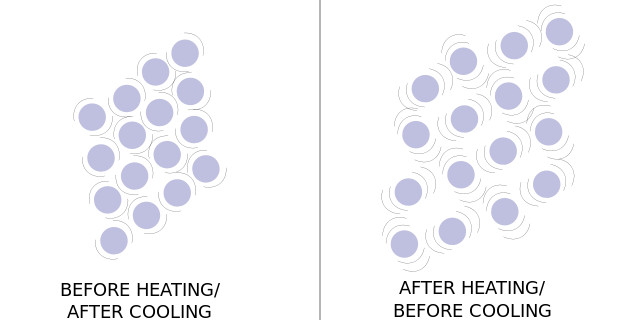
Obrázek 2: schéma atomových vibrací před a po zahřátí.
když se tělo zahřívá, přijímá a ukládá energii do svých atomů ve formě kinetické energie. Toto vystavení zvýšené teplotě způsobuje, že přirozené vibrace atomu rostou silnější a výraznější., Toto zvýšení vibrací tlačí proti mezimolekulárním silám, což umožňuje atomům nebo molekulám stát se dále od sebe a tělo se zvětšuje. Množství, kterým se látka rozpíná v reakci na změnu teploty, je matematicky reprezentováno koeficientem tepelné roztažnosti. Tento koeficient je pro každý materiál jedinečný a je založen na jejich dalších fyzikálních vlastnostech. Čím vyšší je koeficient tepelné roztažnosti materiálu, tím více se rozšíří v reakci na zahřátí., Krystaly mívají nejnižší koeficienty tepelné roztažnosti, protože jejich struktura je velmi jednotná a strukturálně zvuk. Diamant má nejnižší známý koeficient tepelné roztažnosti všech přirozeně se vyskytujících materiálů. Pevné látky s nejvyšší koeficienty tepelné roztažnosti jsou ty, které mají slabý inter-molekulární vazby, typicky polymery, které také mají tendenci mít nízkou teplotou tání. Důvodem je to, že slabší vazby jsou překonány méně vibrační energií., Kovy mají tendenci mít relativně nízkými koeficienty, ale mají také velmi vysokou teplotu tání, a nejsou tak patrné na materiál selhání způsobené stresem z rozšíření. Díky tomu jsou kovy ideální pro použití při měření tepelné roztažnosti.
měření změny objemu způsobené fyzikálním nebo chemickým procesem se nazývá dilatometrie. Přístroj určený k měření změny objemu některé látky se nazývá dilatometr., Nejběžnější příklad dilatometer je rtuťový teploměr, který měří objem a změny v objemu zachycené rtuti, která se používá k určení teploty okolního prostředí. Dilatometry lze také použít k výpočtu koeficientu tepelné roztažnosti. Pro stanovení koeficientu se objem materiálu pečlivě měří, když teplota stoupá z jedné známé hodnoty na druhou. Existuje několik příkladů dilatometrů, které jsou určeny k měření objemu kusů pevných kovů pro stanovení tepelné roztažnosti., Jedním z návrhů jsou kapacitní dilatometry. V tomto provedení je jedna deska kondenzátoru pohyblivá a vzorek je umístěn za ním, takže když se rozšiřuje, tlačí pohyblivou desku blíže k druhé desce. Modernějším a přesnějším příkladem by byl laserový dilatometr, který neustále měří rozměry vzorku pomocí laserů. Jedním z nejvšestrannějších návrhů je optický dilatometr, který je jednoduše digitálním fotoaparátem používajícím optickou skupinu k měření změn velikosti vzorku.,
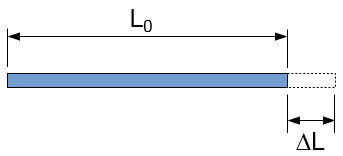
Obrázek 3: diagram ukazující vliv lineární tepelné roztažnosti.
plyny a kapaliny se vždy objemově rozšiřují a rozšiřují se v mezích svých nádob. Teoreticky, pevné látky se vždy rozšiřují také objemově, ale protože drží svůj tvar, zdá se, že se rozšiřují jinak. Například, když se zahřívá dlouhá kovová tyč, její atomy se pohybují dále od sebe ve všech třech rozměrech. Během této expanze bude růst průřezu prutů sotva patrný ve srovnání s jeho růstem podélně., Vzhledem k tomu, že tyč je zpočátku velmi tenká, existuje relativně malý počet atomů, které se tlačí proti sobě ve směru průřezu. V podélném směru však existuje větší počet atomů seřazených, a když se všichni tlačí proti sobě, vytváří řetězovou reakci, která tlačí celkovou délku tyče, aby byla mnohem větší, než byla.
objekty s takovými rozměry lze považovat pouze za rozšiřující se v jedné dimenzi. Předpokládá se, že mají koeficient lineární tepelné roztažnosti namísto koeficientu objemové tepelné roztažnosti., Tento koeficient působí stejně jako trojrozměrný koeficient roztažnosti, s výjimkou, že odpovídá zlomkovému zvýšení délky (místo objemu) na teplotu stupně. Totéž platí o koeficientech rozšíření plochy ve dvou rozměrech pro ploché desky. Z tohoto pozorování lze určit, že množství, které tělo expanduje v reakci na zvýšení teploty, je lineárně závislé na původní velikosti těla.
pozorovací přístup může být přijat najít užitečné rovnice předpovědět výsledné velikosti těla po změně teploty., Jak bylo vysvětleno výše, množství, které se lineární látka rozšiřuje, je lineárně spojeno s původní délkou (L0). Pozorování ukazuje, že expanze je také přibližně lineárně spojena se změnou teploty (dT). Je také zřejmé, že všechny materiály se rozšiřují jinak. Vzhledem k této změně v expanzních vzorcích lze určit, že jiné fyzikální aspekty ovlivňují tepelnou expanzi. Koeficient se používá k zohlednění dalších fyzikálních vlastností látky. Tento koeficient je známý jako koeficient lineární tepelné roztažnosti (α)., Rovnice pro konečné délky by proto mělo být
L = L0 + L0*α*dT
Který může být znovu uspořádány pro α
α = (L – L0)/(L0*dT)
Nebo pokud to je říkal, že změna délky, L – L0, je dL
α = 1/L0 * dL/dT
stejná logika může být použit k vytvoření rovnic o rozšíření objemu. Jsou podobné, s výjimkou délky proměnné by se vyměnily za objem a lineární koeficient roztažnosti by se změnil na volumetrický. Pro zajištění přesnosti je ideální odvodit rovnici rozšíření objemu z lineární rovnice.,
V = L3 = 3
Z analýzy pomocí lineární metody, je zřejmé, že hodnota α je obvykle v ppm rozsahu (x10-6). Vzhledem k tomu, že hodnota je tak malá, oba pojmy, které ji zvyšují na výkon nad jeden výsledek, mají tak malou hodnotu, že na výsledek nebudou mít téměř žádný vliv. Tyto pojmy lze mírně aproximovat.
V = L03
= V0
Protože α je konstantní neznámý koeficient, to může být říkal, že 3α je nový konstantní neznámý koeficient jménem koeficient objemové teplotní roztažnosti, (β).,
V = V0 + V0*β*dT
β = 1/V0 * dV/dT
Tato forma rovnice by nyní být použit k nalezení koeficientů tepelné roztažnosti materiálů, po měření je s dilatometer přes známé změny teploty. Tyto rovnice ukazují, že jak lineární, tak objemové koeficienty mají jednotky Kelvin-1, Celcius-1 nebo Fahrenheit-1.
s dilatometrem a teploměrem je velmi přímočaré provést experiment na vzorku a poté podle rovnice vypočítat koeficienty tepelné roztažnosti., Hliník je vhodným materiálem pro studium touto metodou, protože má velmi vysoký koeficient roztažnosti kovu. Nerezové oceli jsou možná nejčastěji měřeny kvůli jejich hojnému použití v mnoha aplikacích. Tyto oceli mají koeficient, který je pro kovy přibližně průměrný, nicméně nejsou extrémně cenné jako stříbro a zlato. Nedostatek tepelných znalostí během inženýrství a designu může vést ke zhroucení mostů nebo zničení cenného vybavení., Tepelná roztažnost materiálů může být hlavním zátarasem pro stavbu a projektování, nicméně mnoho aplikačních procesů a technologií bylo navrženo s tepelnou roztažností jako základní součást funkce.

Obrázek 4: Dilatační spáry na mostě,
