sekvence
sekvence je sada věcí (obvykle čísel), které jsou v pořádku.
geometrické sekvence
v geometrické sekvenci se každý termín nachází vynásobením předchozího výrazu konstantou.
obecně píšeme geometrickou sekvenci takto:
{a, ar, ar2, ar3,…, }
kde:
- první termín
- r je faktor mezi podmínkami (tzv. „společného poměru“)
Ale pozor, r nesmí být 0.
- , Kdy r=0, dostaneme posloupnost {a,0,0,…}, která není geometrická
Pravidlo
můžeme také vypočítat libovolný výraz pomocí Pravidlo:
xn = ar(n-1)
(používáme „n-1“, protože ar0 je pro 1. termín)
Geometrické Posloupnosti mohou mít také menší a menší hodnoty:
Příklad:
4, 2, 1, 0.5, 0.25, …,
tato sekvence má faktor 0,5 (a půl) mezi každým číslem.
jeho pravidlem je xn = 4 × (0,5)n-1
proč“ geometrická “ sekvence?,
Protože to je, jako zvýšení rozměrů v geometrii:
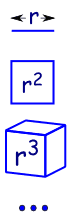 |
čára je 1-dimenzionální a má délku r |
| v 2 rozměry čtverce má rozlohu r2 | |
| ve 3 rozměrech krychle má objem r3 | |
| atd (ano, můžeme mít 4 a více rozměry v matematice)., |
Geometrické Posloupnosti jsou někdy nazývána Geometrické Posloupnosti (G. P.)
Součet Geometrické Řady
součet těchto:
a + ar + ar2 + … + ar(n-1)
(Každý termín je archa, kde k začíná na 0 a jde do n-1)
můžeme použít tento šikovný vzorec:

první termín
r je společné „poměr“ mezi pojmy
n je počet termínů,
Co je na tom vtipného Σ symbol?, To se nazývá Sigma Notace
| (tzv. Sigma) znamená „shrnul“ |
A pod a nad ním jsou zobrazeny počáteční a koncové hodnoty:
To říká, „shrnul n kde n jde od 1 do 4. Odpověď=10
vzorec se snadno používá …, „plug in“ hodnoty a, r a n.
je Použití Vzorce
podívejme se na vzorec v akci:
Příklad: Zrna Rýže na šachovnici

Na stránce Binární Číslice, jsme dát příklad zrnek rýže na šachovnici. Je položena otázka:
Když jsme místo rýže na šachovnici:
- 1 obilí na první políčko,
- 2 zrna na druhý čtverec,
- 4 zrnka, na třetí a tak dále,
- …
… zdvojnásobení zrn rýže na každém čtverci …
…, kolik zrn rýže celkem?
Takže máme:
- a = 1 (první termín)
- r = 2 (čtyřhry pokaždé)
- n = 64 (64 čtverců na šachovnici)
:

to se Stane:
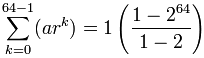
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Což byl přesně ten výsledek, který jsme dostali na Binární Číslice stránku (díky bohu!)
a další příklad, tentokrát s r méně než 1:
proč vzorec funguje?,
podívejme se, proč vzorec funguje, protože používáme zajímavý „trik“, který stojí za to vědět.
Všimněte si, že S A S·r jsou podobné?
nyní je odečtěte!
Wow! Všechny podmínky uprostřed úhledně vyruší.,
(Což je pěkný trik)
odečtením S·r z Y dostaneme jednoduchý výsledek:
S − S·r = a − arn
Pojďme uspořádat ji najít S:
Což je náš vzorec (ta-da!):

nekonečná Geometrická řada
co se stane, když n přejde do nekonečna?,
můžeme použít tento vzorec:
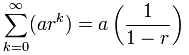
Ale pozor:
r musí být mezi (ale ne včetně) -1 a 1,
a r by neměly být 0, protože posloupnost {a,0,0,…} není geometrický
naše infnite geometrická řada má konečný součet, když je poměr menší než 1 (a větší než -1)
vraťme se k naší předchozí příklad, a uvidíme, co se stane:
|
nevěříte mi? Stačí se podívat na tento čtverec: přidáním 12 + 14 + 18 + … skončíme s celou věcí!, |
 |
Opakující se Desetinná
Na další stránce jsme se ptali, „Má 0.999… rovno 1?“, no, uvidíme, jestli to dokážeme vypočítat:



