Rychlá Odpověď:
Pro pravoúhlý trojúhelník:

funkce sinus sin trvá úhel θ a dává poměr protilehlé přepony
inverzní funkci sinus sin-1 má poměr oppositehypotenuse a dává úhel θ
A kosinus a tangens následovat podobný nápad.,
a nyní pro podrobnosti:
sinus, kosinus a tečna jsou založeny na pravoúhlém trojúhelníku
jsou to velmi podobné funkce … takže se podíváme na funkci sinus a pak inverzní sinus, abychom se dozvěděli, o čem to všechno je.,
Sinus Funkce
Sinus úhlu θ, je:
- délka strana Naproti úhlu θ
- vydělená délkou Přepony
Nebo, více jednoduše:
sin(θ) = Protilehlá / Přepona
Funkce Sinus nám může pomoci vyřešit věci, jako je tento:
Inverzní Sinus Funkce
Ale někdy je úhel musíme najít.
zde přichází „inverzní sinus“.
odpovídá na otázku “ jaký úhel má sinus rovný opačné / hypotenuse?,“
symbol pro inverzní sinus je sin-1 nebo někdy arcsin.
jsou jako dopředu a dozadu!

- hřích vyžaduje úhlu a dává nám poměr „protilehlá/přepona“
- sin-1 má poměr „protilehlá/přepona“ a dává nám úhlu.
příklad:
Kalkulačka
 |
kalkulačka, stiskněte jednu z následujících možností (v závislosti na značku kalkulačka):buď 2ndF hřích „nebo“ shift sin‘. |
Na kalkulačce, zkusit pomocí hříchu a pak sin-1, aby viděli, co se stane,
Více Než Jednoho Úhlu!
inverzní sinus zobrazuje pouze jeden úhel … ale existuje více úhlů, které by mohly fungovat.
příklad: zde jsou dva úhly, kde opak / přepona = 0.,5
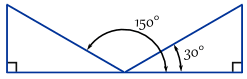
Ve skutečnosti existuje nekonečně mnoho úhlů, protože můžete držet přidání (nebo odečtením) 360°:
Pamatujte si to, protože tam jsou časy, kdy budete skutečně potřebovat jeden z dalších úhlů!
Shrnutí
Sinus úhlu θ, je:
sin(θ) = Protilehlá / Přepona
A Inverzní Sinus je :
sin-1 (Protilehlá / Přepona) = θ
Co „, protože“ a „tan“ … ?
přesně stejný nápad, ale různé boční poměry.,
Cosinus
Kosinus úhlu θ je:
cos(θ) = Přilehlá / Přepona
A Inverzní Kosinus je :
cos-1 (Přilehlá / Přepona) = θ
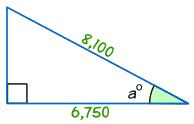
Příklad: Najděte velikost úhlu a°
protože° = Přilehlá / Přepona
protože° = je 6750/8,100 = 0.8333…
a° = cos-1 (0, 8333…) = 33.,6° (na 1 desetinné místo)
Tečně
Tangens úhlu θ je:
tan(θ) = Protilehlá / Přilehlá.
Takže Inverzní Tangens je :
tan-1 (Protilehlá / Přilehlá) = θ
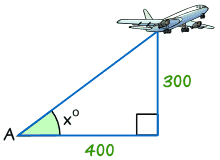
Příklad: Zjistit velikost úhlu x°
tan x° = Protilehlá / Přilehlá.
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (správně na 1 desetinné místo)
Další Jména
Někdy sin-1, se nazývá asin nebo arcsin
Podobně, protože-1 se nazývá acos nebo arccos
A tan-1 se nazývá atan nebo arkus tangens
Příklady:
- arcsin(y) je stejný jako sin-1(y)
- atan(θ) je stejný jako tan-1(θ)
- atd.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- ale inverzní sinus a inverzní kosinus „nepokračují navždy“ jako sinus a kosinus…
podívejme se na příklad Kosinu.
Tady je Kosinus a Inverzní Kosinus vyneseny na stejném grafu:
Kosinus a Inverzní Kosinus.
jsou to zrcadlové obrazy (o diagonální)
Ale proč Inverzní Kosinus usekli v horní a dolní části (ty tečky jsou opravdu součástí funkce) … ?
protože je to funkce, může dát pouze jednu odpověď
, když se zeptáme “ co je cos-1 (x) ?,“
Jedna Odpověď, nebo Nekonečně Mnoho Odpovědí
Ale viděli jsme dříve, že existuje nekonečně mnoho odpovědí, a tečkovaná čára na grafu to ukazuje.
takže ano existuje nekonečně mnoho odpovědí …
… ale představte si, že do kalkulačky zadáte 0.5, stiskněte cos-1 a dává vám nekonečný seznam možných odpovědí …
takže máme toto pravidlo, že funkce může dát pouze jednu odpověď.
takže tím, že ji odřízneme, dostaneme jen jednu odpověď, ale měli bychom si uvědomit, že by mohly existovat další odpovědi.,
tečna a inverzní tečna
a zde je tečna a inverzní tečna. Můžete vidět, jak jsou zrcadlové obrazy (o diagonále) …?

Tečně

Inverzní Tangens



