nejjednodušší způsob, jak zachytit myšlenku rostoucí populace je s jednobuněčných organismů, jako jsou bakterie nebo cilliate. Na obrázku 1 je zobrazena populace paramecia v malém laboratorním skluzu deprese. V této populaci se jednotlivci dělí jednou denně. Takže, počínaje jediným jedincem v den 0, očekáváme, v následujících dnech, 2, 4, 8, 16, 32, a 64 jedinců v populaci., Zde můžeme vidět, že, na konkrétní den, počet jedinců v populaci je prostě dvakrát tolik, než počet byl den předtím, takže počet dnes, nazývat N(dnes), je rovna dvojnásobku číslo včera, říkají N(včera), což můžeme napsat více kompaktně jako N(dnes) = 2N(včera).
takže má smysl psát to jako, N(t) = 2n (t – 1), kde T může mít jakoukoli hodnotu vůbec.,
Nyní můžeme zobecnit tuto myšlenku trochu, když jsme na vědomí, že v den, šest číslo je rovno dvojnásobku počtu na den pět, nebo N(6) = 2N(5) a na den pět počet je roven dvojnásobku počtu na den čtyři, nebo N(5) = 2N(4), atd.
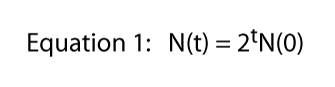
kde t znamená Kdykoli (např., pokud T = 6, N(6) = 26).
nakonec si všimneme, že tato rovnice byla odvozena od konkrétní situace znázorněné na obrázku 1, kde jedno rozdělení za den bylo tvrdé a rychlé pravidlo., To je místo, kde 2 pochází z rovnice 1 — z každého jednotlivého paramecia získáme dva jednotlivce následující den. Samozřejmě, že míra rozdělení může být cokoliv. Pokud by existovaly dvě divize denně, ale jedna buňka vždy zemřela, očekávali bychom, že tři jedinci od každého jednotlivce a rovnice 1 by byla N(t) = 3tN(0)., Takže rozdělení sazba by mohla být jakékoliv číslo a obecné rovnice se stává,
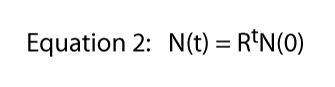
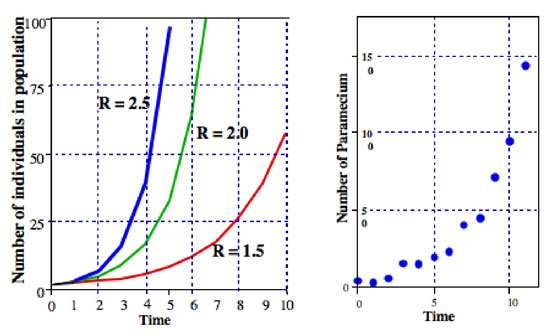
, kde R je obvykle nazývá konečná míra růstu populace (v konkrétním případě dělení Trepka konečných míra růstu populace je rovna rozdělení frekvence). Na Obrázku 2 můžeme ilustrovat této rovnice pro různé hodnoty R. To je obvykle odkazoval se na jako exponenciální rovnice, a formu dat na Obrázku 2 je obecná forma se nazývá exponenciální.,
Jakoukoliv hodnotu R může být reprezentován v nekonečně mnoha způsoby (např. je-li R = 16, můžeme psát R = 8 x 2, nebo R = 42, nebo R = 32/2, nebo R = 2.718282.77). Ten poslední výraz (R = 2.718282.,77) využívá důležitou konstantu, kterou lze připomenout z elementárního počtu, Eulerovy konstanty. Vyjádření jakékoli hodnoty R jako Eulerovy konstanty zvýšené na nějakou sílu je ve skutečnosti velmi užitečné-přináší do obrazu plnou sílu kalkulu.,olize Eulerova konstanta e můžeme napsat Rovnice 2
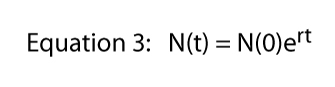
Nyní vezmeme přirozený logaritmus obou stran Rovnice 3 — pamatujte si, ln(ex) = x — Rovnice 3 se stává: ln = ln + rt
A když jsme začali populace s jednoho jedince (jako v příkladu výše), máme

ze které vidíme, že přirozený logaritmus z počtu obyvatel, v jakémkoli čase, je nějaká konstanta, krát čas., Konstanta r se označuje jako vnitřní rychlost přirozeného nárůstu (Obrázek 2).
všechny druhy mikroorganismů vykazují vzory, které jsou velmi blízké exponenciálnímu růstu populace. Například v pravém grafu obrázku 2 je populace paramecia rostoucí v laboratorní kultuře. Vzor růstu je velmi blízko vzoru exponenciální rovnice.
Další způsob zápisu exponenciální rovnice je jako diferenciální rovnice, tj., Spíše než se ptát, co je velikost populace v čase t, ptáme se, co je rychlost, při které populace roste v čase t. Rychlost je symbolizovaná jako dN/dt, což jednoduše znamená „změna v N relativní změna v t,“ a pokud si vzpomínám, vaše základní kalkul, můžeme najít tempo růstu mezi sebou diferenciací Rovnice 4, což nám dává
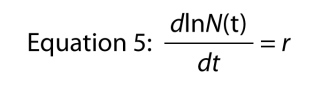
což je docela pozoruhodné, protože to říká, že míra růstu log počtu v populaci je konstantní., Tato konstantní rychlost růstu logu populace je vnitřní míra nárůstu.,
Připomeňme si, že rychlost změny protokolu o čísla je stejný jako „na hlavu“ změna v tom, že číslo, což znamená, že můžeme napsat Rovnice 5 jako

kde jsme vynechat proměnné t, neboť je zřejmé, kam to vede, a pak jsme se uspořádat trochu
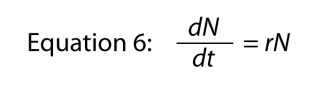
, kde parametr r je vnitřní míra přirozeného přírůstku., Základní vztah mezi konečnou rychlostí zvýšení a vnitřní rychlostí je
r = ln(R)
, kde ln odkazuje na přirozený logaritmus. Všimněte si, že Rovnice 6 a Rovnice 3 jsou jen různé formy téže rovnice (Rovnice 3 je integrované formě Rovnice 6; Rovnice 6 je diferencovaná forma Rovnice 3), a oba mohou být odkazoval se na jednoduše jako exponenciální rovnice.,

exponenciální rovnice je užitečným modelem jednoduchých populací, alespoň po relativně krátkou dobu., Například, pokud laborant potřebuje vědět, kdy bakteriální kultury dosáhne určité hustoty obyvatelstva, exponenciální rovnice může být použit pro předpověď, jak se přesně, kdy to velikost populace bude dosaženo. Dalším příkladem je případ zemědělských škůdců. Býložravci jsou pro rostliny vždy potenciálně hlavními problémy. Pokud jsou rostliny vystavené takovým ohniskům zemědělské, což znamená plodiny, ztráta může být velmi významná jak pro zemědělce, tak pro spotřebitele. Existuje tedy vždy tlak na prevenci takových ohnisek., Od druhé světové války hlavní zbraní v boji proti takovým ohniskům škůdců byly chemické pesticidy, jako je DDT. V posledních letech jsme si však uvědomili, že tyto pesticidy jsou z dlouhodobého hlediska extrémně nebezpečné jak pro životní prostředí, tak pro lidi. V důsledku toho došlo k pohybu k omezení množství pesticidů, které jsou postříkány k boji proti škůdcům. Hlavním způsobem, jak toho dosáhnout, je stanovit ekonomický práh, kterým je hustota obyvatelstva potenciálního škůdce, pod nímž je poškození plodiny nevýznamné (tj., Když pest populace vzroste nad tuto hranici, zemědělec musí přijmout opatření a použít nějaký druh pesticidu, nebo jiné prostředky kontrole škůdců. Vzhledem k povaze tohoto problému je někdy nanejvýš důležité předvídat, kdy škůdce dosáhne ekonomického prahu. Znalost R pro druhy škůdců umožňuje zemědělci předvídat, kdy bude nutné použít nějaký druh kontrolního postupu (obrázek 3).
exponenciální rovnice je také užitečným modelem pro rozvoj intuitivních představ o populacích., Klasickým příkladem je rybník s populací lilie. Pokud každý lily pad reprodukuje sám (dvě podložky se místo, kde jeden pad byl) každý měsíc, a to trvalo, řekněme, tři roky u rybníka, aby se stal z poloviny naplněné lilie podložky, jak dlouho bude trvat, rybník, aby byly zcela pokryt s lily podložky? Pokud nepřestanete přemýšlet příliš jasně, je lákavé říci, že to bude trvat stejně dlouho, tři roky, než se druhá polovina rybníka stane tak naplněnou jako první. Odpověď je samozřejmě jeden měsíc.,
dalším populárním příkladem je příslovečný staroegyptský (nebo někdy perský) matematik, který žádá od krále platbu ve formě zrn pšenice (někdy rýže). Jedno zrno na prvním čtverci šachovnice, dvě zrna na druhém náměstí a tak dále, až do posledního čtverce. Faraon si nedokáže představit, že by taková jednoduchá platba mohla činit mnoho, a tak souhlasí. Exponenciální růst však plně neocenil., Protože tam jsou 64 čtverců na šachovnici, můžeme použít Rovnici 2 určit, jak mnoho zrna pšenice bude muset zaplatit na poslední metr (R zvýšen na 64. energie, což je o 18,446,744,074,000,000,000 — hodně pšenice, skutečně, rozhodně víc než v celém království). Tyto příklady zdůrazňují často překvapivý způsob, jakým exponenciální proces může vést k velmi velkému počtu velmi rychle.
