Nonagon (Čeština)

nonagon je polygon, který má devět stran. Na obrázku níže je několik typů neagonů.

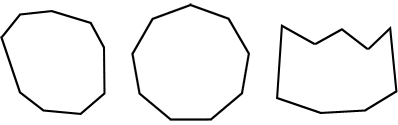
Nonagon klasifikace

stejně Jako ostatní polygony, nonagon mohou být klasifikovány jako pravidelný nebo nepravidelný. Pokud jsou všechny strany a vnitřní úhly nonagonu stejné, je to pravidelný nonagon. Jinak se jedná o nepravidelný nonagon.,

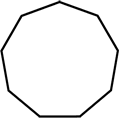
Pravidelné nonagon	Nepravidelné nonagon
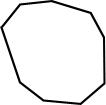Všechny strany a vnitřní úhly jsou shodné	Ne všechny strany a úhly jsou shodné

Nonagons a další polygony mohou být také klasifikovány jako buď konvexní, nebo konkávní. Pokud jsou všechny vnitřní úhly nonagonu menší než 180°, je konvexní. Pokud je jeden nebo více vnitřních úhlů větší než 180°, je konkávní. Pravidelný nonagon je konvexní nonagon.,

Konvexní nonagon	Konkávní nonagon
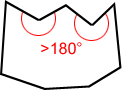Všechny vnitřní úhly < 180°	Jeden nebo více vnitřních úhlů > 180°

Úhlopříčky nonagon

úhlopříčka je úsečka spojující dva non-po sobě jdoucích vrcholů. Pro nonagon lze nakreslit celkem dvacet sedm různých úhlopříček. Následující obrázek je příkladem.,

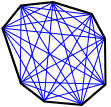
k Dispozici je 6 úhlopříček rozšíření z každého z 9 vrcholů nonagon nad vytvářet celkem 27 úhlopříček.

vnitřní úhly nonagonu

součet vnitřních úhlů nonagonu se rovná 1260°.

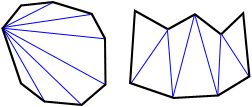
, Jak je znázorněno na obrázku výše, šest úhlopříček lze vyvodit rozdělit nonagon do sedmi trojúhelníky. Modré čáry nahoře ukazují jen jeden způsob, jak rozdělit nonagon na trojúhelníky; existují i jiné., Součet vnitřních úhlů sedmi trojúhelníků se rovná součtu vnitřních úhlů nonagonu. Protože součet vnitřních úhlů trojúhelníku je 180°, součet vnitřních úhlů nonagon je 9 × 180° = 1260°.

Regular nonagon

pravidelný nonagon je nonagon, ve kterém mají všechny strany stejnou délku a všechny vnitřní úhly mají stejnou míru.

Úhly pravidelné nonagon

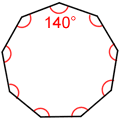
Od každé z devíti vnitřních úhlů v pravidelné nonagon jsou si rovni v opatření, že každý vnitřní úhel opatření 1260° ÷ 9 = 140°, jak je znázorněno níže.,

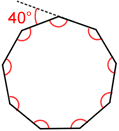
Každý vnější úhel pravidelné nonagon má stejnou míru 40°.

Symetrie v pravidelné nonagon

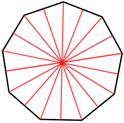
pravidelné nonagon má 9 řádků, symetrie a rotační symetrie, řád 9, což znamená, že to může být otočen takovým způsobem, že to bude vypadat stejně jako původní tvar 9 krát v 360°.,

Lines of symmetry	Rotational symmetry
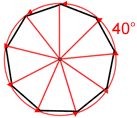9 lines of symmetry	Nine 40° of rotation about the center.