Statistiky 2 – Korelační Koeficient a Koeficient Determinace

Korelační Koeficient

Jak se vaše regresní rovnice opravdu představují
vaše sada dat?
jedním ze způsobů, jak určit odpověď na tuto otázku, je zkouška korelačního koeficientu a koeficientu stanovení.,

množství r, se nazývá lineární korelační koeficient, který měří sílu a
směr lineární vztah mezi dvěma proměnnými. Koeficient lineární korelace
je někdy označován jako korelační koeficient Pearsonova momentu produktu v
cti jeho vývojáře Karla Pearsona.
matematický vzorec pro computingr je: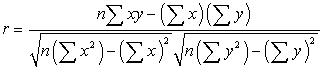

, kde n je počet párů dat.,
(nejste rádi, že máte grafickou kalkulačku, která vypočítá tento vzorec?)
hodnota r je taková, že -1 < r < +1. Znaky + a – se používají pro pozitivní lineární korelace
a negativní lineární korelace.
pozitivní korelace: pokud x a y mají silnou pozitivní lineární korelaci, r je blízko
K +1. Hodnota R přesně +1 znamená perfektní pozitivní fit., Kladné hodnoty
označují vztah mezi proměnnými x a y tak, že se hodnoty pro X zvyšují, hodnoty
Pro y se také zvyšují.
negativní korelace: pokud x a y mají silnou negativní lineární korelaci, r je blízko
k -1. Hodnota r přesně -1 znamená perfektní negativní fit. Záporné hodnoty
označují vztah mezi x a y tak, že jako hodnoty pro zvýšení X se hodnoty
Pro y snižují.
žádná korelace: pokud neexistuje lineární korelace nebo slabá lineární korelace, r je
blízko 0., Hodnoty blízké nule, znamená to, že tam je náhodný, nelineární vztah
mezi dvěma proměnnými
Všimněte si, že r je bezrozměrná veličina; to znamená, že nezávisí na jednotkách
zaměstnání.
dokonalá korelace ± 1 nastává pouze tehdy, když datové body leží přesně na přímce
. Pokud je R = +1, sklon této čáry je pozitivní. Pokud je R = -1, sklon této
čáry je záporný.
korelace větší než 0.8 je obecně popisována jako silná, zatímco korelace
menší než 0.,5 je obecně popsán jakoslabé. Tyto hodnoty se mohou lišit podle
„typu“ zkoumaných dat. Studie využívající vědecké údaje může vyžadovat silnější korelaci
než studie využívající údaje o sociálních vědách.

koeficient determinace, r 2,je užitečné, protože to dává podíl
odchylka (fluktuace) jedné proměnné, která je předvídatelná od jiné proměnné.,
jedná se o opatření, které nám umožňuje určit, jak jistý může být při vytváření předpovědí
z určitého modelu/grafu.
koeficient stanovení je poměr vysvětlené variace k celkové variaci
.
koeficient determinace je taková, že 0 < r 2 < 1, a označuje sílu
lineární vztah mezi x a y.,
koeficient stanovení představuje procento dat, která je nejblíže
k linii best fit. Například, je-li r = 0.922, pak r 2 = 0.850, což znamená, že
85% z celkové variability iny lze vysvětlit tím, že lineární vztah mezi x,
a y (jak je popsáno v regresní rovnici). Zbylých 15% celkové odchylky
V y zůstává nevysvětleno.
koeficient stanovení je měřítkem toho, jak dobře regresní čára
reprezentuje data., Pokud regresní čára prochází přesně každým bodem na grafu rozptylu
, bude schopna vysvětlit všechny variace. Čím dále je řádek
od bodů, tím méně je schopen vysvětlit.