
V tomto článku se dozvíte o SVM nebo Support Vector Machine, která je jedním z nejvíce populární AI algoritmů (je to jeden z top 10 AI algoritmy) a o Kernel Trik, který se zabývá non-linearity a vyšší rozměry., Budeme se dotýkat témat jako nadrovin, Lagrangeovy Multiplikátory, budeme mít vizuální příklady a příklady kódu (podobný příklad kódu používá v KNN kapitole) pro lepší pochopení tohoto velmi důležitého algoritmu.
SVM vysvětleno
podpůrný vektorový stroj je algoritmus učení pod dohledem, který se většinou používá pro klasifikaci, ale může být použit také pro regresi. Hlavní myšlenkou je, že na základě označených dat (tréninkových dat) se algoritmus snaží najít optimální hyperplane, kterou lze použít ke klasifikaci nových datových bodů. Ve dvou rozměrech je hyperplane jednoduchá čára.,
Obvykle učící algoritmus se snaží naučit co nejvíce společných vlastností (to, co odlišuje jednu třídu od druhé) třídy a klasifikace je založena na těchto reprezentativních charakteristik naučil (takže klasifikace je založena na rozdílech mezi třídami). SVM funguje naopak. Najde nejpodobnější příklady mezi třídami. To budou podpůrné vektory.
jako příklad můžeme zvážit dvě třídy, jablka a citrony.,
další algoritmy se naučí nejzřetelnější, nejreprezentativnější vlastnosti jablek a citronů, jako jablka jsou zelená a zaoblená, zatímco citrony jsou žluté a mají eliptickou formu.
naproti tomu SVM bude hledat jablka, která jsou velmi podobná citronům, například jablka, která jsou žlutá a mají eliptickou formu. Bude to podpůrný vektor. Dalším podpůrným vektorem bude citron podobný jablku (zelený a zaoblený). Takže jiné algoritmy se učí rozdíly, zatímco SVM učí podobnosti.,
Pokud se podíváme na výše uvedený příklad ve 2D, budeme mít něco jako toto:

a Jak jdeme zleva doprava, všechny příklady, které budou klasifikovány jako jablka do dosažení žluté jablko. Od tohoto okamžiku důvěra, že novým příkladem je jablko, klesá, zatímco důvěra citronové třídy se zvyšuje., Když se důvěra citronové třídy stane větší než důvěra třídy apple, budou nové příklady klasifikovány jako citrony (někde mezi žlutým jablkem a zeleným citronem).
na základě těchto podpůrných vektorů se algoritmus snaží najít nejlepší hyperplane, která odděluje třídy. Ve 2D je nadrovina je lineární, takže by to vypadalo takto:

Ok, ale proč jsem nakreslil modrou hranice, jako je na obrázku výše?, Také bych mohl nakreslit hranice, jako je tento:

Jak můžete vidět, máme nekonečné množství možností, jak kreslit rozhodovací hranice. Jak tedy můžeme najít optimální?
nalezení optimální Hyperplane
intuitivně nejlepší linie je čára, která je daleko od příkladů jablek i citronu (má největší rezervu)., Abychom měli optimální řešení, musíme maximalizovat marži oběma způsoby (pokud máme více tříd, musíme ji maximalizovat s ohledem na každou z tříd).

Takže pokud můžeme porovnat na obrázku výše se na obrázek níže, můžeme snadno pozorovat, že první je optimální nadrovina (přímka) a druhý je sub-optimální řešení, protože marže je daleko kratší.,

Protože chceme maximalizovat rozpětí bere v úvahu všechny třídy, namísto jednoho pro každou třídu, jsme použili „globální“ marže, která bere v úvahu všechny třídy., Toto rozpětí by vypadat jako fialová čára na následujícím obrázku:

Toto rozpětí je ortogonální k hranici a ve stejné vzdálenosti na podporu vektorů.
takže kde máme vektory? Každý z výpočtů (výpočet vzdálenosti a optimální nadroviny) jsou vyrobeny v vektorový prostor, takže každý datový bod je považován za vektor. Rozměr prostoru je definován počtem atributů příkladů., Chcete-li pochopit matematiku za, přečtěte si prosím tento stručný matematický popis vektorů, hyperplanes a optimalizace: SVM stručně.
všechny podporované vektory jsou datové body, které definují polohu a okraj nadroviny. Říkáme jim „podpůrné“ vektory, protože to jsou reprezentativní datové body tříd, pokud přesuneme jeden z nich, změní se pozice a/nebo marže. Přesun dalších datových bodů nebude mít vliv na marži nebo pozici nadroviny.,
abychom mohli klasifikovat, nepotřebujeme všechny tréninkové datové body (jako v případě KNN), musíme uložit pouze podpůrné vektory. V nejhorším případě budou všechny body podporovat vektory, ale to je velmi vzácné a pokud se to stane, měli byste zkontrolovat model pro chyby nebo chyby.
takže učení je v podstatě ekvivalentní s nalezením hyperplane s nejlepším okrajem, takže je to jednoduchý optimalizační problém.,/h2>
základní kroky SVM jsou:
- vyberte dvě nadroviny (v 2D), které odděluje data bez bodů mezi nimi (červená linie)
- maximalizovat jejich vzdálenost (rozpětí)
- průměr linky (linka na půl cesty mezi dvě červené čáry) bude rozhodnutí ohraničení
Tohle je velmi příjemné a snadné, ale najít nejlepší marži, problém optimalizace není triviální (je to snadné v 2D, kdy máme pouze dva atributy, ale co když máme N rozměrech, kde N je velmi velké číslo)
jak vyřešit optimalizační problém, použijeme Lagrangeovy Multiplikátory., Pochopit tuto techniku můžete si přečíst tyto dva články: Dualita Langrange Multiplikátor a Jednoduché Vysvětlení, Proč Langrange Multiplikátory Wroks.
dosud jsme měli lineárně oddělitelná data, takže jsme mohli použít čáru jako hranici třídy. Ale co když se musíme vypořádat s nelineárními datovými sadami?,
SVM na nelineární Datové Sady
příklad nelineární dat je:

V tomto případě nemůžeme najít přímku oddělit jablka od citronů. Tak jak můžeme vyřešit tento problém. Použijeme trik jádra!
základní myšlenkou je, že když je datová sada neoddělitelná v aktuálních rozměrech, přidejte další rozměr, možná tak budou data oddělitelná., Jen o tom přemýšlejte, výše uvedený příklad je ve 2D a je neoddělitelný, ale možná ve 3D existuje mezera mezi jablky a citrony, možná existuje rozdíl na úrovni, takže citrony jsou na úrovni jedna a citrony jsou na úrovni dvě. V tomto případě můžeme snadno nakreslit oddělovací hyperplane (ve 3D je hyperplane rovinou) mezi úrovní 1 a 2.
mapování na vyšší rozměry
abychom tento problém vyřešili, neměli bychom jen slepě přidávat další rozměr, měli bychom prostor transformovat, abychom tento rozdíl úrovně generovali úmyslně.,
mapování z 2D na 3D
předpokládejme, že přidáme další rozměr zvaný X3. Další důležitou transformací je, že v nové dimenzi jsou body organizovány pomocí tohoto vzorce x12 + x22.
Pokud jsme pozemek na rovině definované x2 + y2 vzorec, dostaneme něco jako toto:

Teď musíme mapě jablka a citrony (které jsou jen jednoduché body) do tohoto nového prostoru. Přemýšlejte o tom pečlivě, co jsme udělali?, Právě jsme použili transformaci, ve které jsme přidali úrovně založené na vzdálenosti. Pokud jste v původu, budou body na nejnižší úrovni. Když se vzdalujeme od původu, znamená to, že stoupáme na kopec (pohybujeme se od středu roviny směrem k okrajům), takže úroveň bodů bude vyšší., Pokud vezmeme v úvahu, že původ je citron od centra, budeme mít něco jako toto:
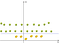
Nyní můžeme snadno oddělit dvě třídy. Tyto transformace se nazývají jádra. Populární jádra jsou: Polynomiální Kernel, Gaussovo Jádro, Radial Basis Function (RBF), Laplaceova RBF Kernel, Esovité Jádro, Anove RBF Kernel, atd. (viz Funkce Jádra nebo podrobnější popis Strojového Učení Jader).,
Mapování z 1D do 2D
Další, jednodušší příklad ve 2D by to být:

Po použití jádra a po všech transformací dostaneme:

po transformaci, můžeme snadno vymezit dvě třídy pomocí jen jeden řádek.,
v aplikacích v reálném životě nebudeme mít jednoduchou přímku, ale budeme mít spoustu křivek a vysokých rozměrů. V některých případech nebudeme mít dvě nadroviny, které oddělují data bez bodů mezi nimi, takže potřebujeme nějaké kompromisy, toleranci pro odlehlé hodnoty. Naštěstí SVM algoritmus má tzv. regularizace parametr konfigurace trade-off a tolerovat extrémy.
Parametry Ladění
Jak jsme viděli v předchozí části výběr správného jádra je zásadní, protože pokud transformace je nesprávné, pak model může mít velmi špatné výsledky., Zpravidla vždy zkontrolujte, zda máte lineární data a v takovém případě vždy používejte lineární SVM (lineární jádro). Lineární SVM je parametrický model, ale RBF jádro SVM není, takže složitost druhé roste s velikostí tréninkové sady. Nejen, že je dražší vycvičit RBF jádra SVM, ale budete také muset udržet jádro matice kolem, a projekce do této „nekonečné“ vyšší dimenzionální prostor, kde se data stanou lineárně oddělitelné, je dražší, stejně během předpověď., Kromě toho máte více hyperparametrů, takže výběr modelu je také dražší! A konečně je mnohem snazší překonat složitý model!
Regularizace
parametr Regularizace (v Pythonu se nazývá C) říká optimalizaci SVM, jak moc se chcete vyhnout vynechání klasifikace každého příkladu školení.
Pokud je C vyšší, Optimalizace zvolí menší hyperplane marže, takže tréninková data miss klasifikační rychlost bude nižší.,
na druhou stranu, pokud je C nízká, pak bude marže velká, i když budou chybět klasifikované příklady tréninkových dat. To je znázorněno v následujících dvou grafech:

Jak můžete vidět na obrázku, až C je nízká, marže je vyšší (tak implicitně nemáme tolik křivky, linie není striktně dodržuje datových bodů), i když dvě jablka byly klasifikovány jako citrony., Když je C vysoká, hranice je plná křivek a všechna tréninková data byla správně klasifikována. Nezapomeňte, že i když všechny přípravy dat byl správně klasifikován, neznamená to, že zvýšení C bude vždy zvýšit přesnost (protože overfitting).
Gamma
dalším důležitým parametrem je Gamma. Parametr gama definuje, jak daleko dosahuje vliv jediného příkladu výcviku. To znamená, že vysoká Gama zváží pouze body blízké věrohodné hyperplane a nízká Gama bude zvažovat body ve větší vzdálenosti.,

Jak můžete vidět, snížení Gama výsledkem bude, že nalezení správné nadroviny zváží bodů na větší vzdálenosti, takže stále více a více bodů budou použity (zelená linie ukazuje, které body byly považovány za při nalezení optimální nadroviny).
Margin
posledním parametrem je marže. Už jsme mluvili o marži, vyšší marže výsledky lepší model, takže lepší klasifikace (nebo predikce)., Marže by měla být vždy maximalizována.
SVM příklad pomocí Pythonu
v tomto příkladu použijeme Social_Networks_Ads.soubor csv, stejný soubor jako v předchozím článku, viz příklad KNN pomocí Pythonu.
v tomto příkladu zapíšu pouze rozdíly mezi SVM a KNN, protože se nechci opakovat v každém článku! Pokud chcete celé vysvětlení o tom, jak můžeme číst sadu dat, jak analyzovat a rozdělit naše data nebo jak můžeme vyhodnotit nebo vykreslit hranice rozhodnutí, přečtěte si příklad kódu z předchozí kapitoly (KNN)!,
protože Knihovna sklearn je velmi dobře napsaná a užitečná knihovna Python, nemáme příliš mnoho kódu na změnu. Jediný rozdíl spočívá v tom, že musíme importovat třídu SVC (SVC = SVM ve sklearnu) ze sklearnu.svm místo třídy KNeighborsClassifier ze sklearnu.souseda.
po importu SVC můžeme vytvořit náš nový model pomocí předdefinovaného konstruktoru. Tento Konstruktor má mnoho parametrů, ale popíšu pouze ty nejdůležitější, většinou nebudete používat jiné parametry.,
nejdůležitější parametry jsou:
- jádro: typ jádra, který má být použit. Nejběžnější jádra jsou rbf (toto je výchozí hodnota), poly nebo sigmoid, ale můžete si také vytvořit vlastní jádro.,
- C: to je parametr regularizace je popsáno v Tuning sekci Parametry
- gama: to bylo také popsáno v Tuning sekci Parametry
- míry: používá se pouze tehdy, když zvolené jádro poly a nastaví stupeň polinom
- pravděpodobnost: to je logický parametr, a pokud je to pravda, pak model se vrátí pro každý předpověď vektor pravděpodobnosti příslušnosti do jednotlivých tříd proměnné odezvy. Takže v podstatě vám poskytne důvěru pro každou předpověď.,
- smršťování: to ukazuje, zda chcete, aby se zmenšující heuristika používala při optimalizaci SVM, která se používá při sekvenční minimální optimalizaci. Je to výchozí hodnota je pravda, pokud nemáte dobrý důvod, prosím, neměňte tuto hodnotu na false, protože zmenšuje bude výrazně zlepšit svůj výkon, pro velmi malé ztráty, pokud jde o přesnost ve většině případů.
nyní umožňuje vidět výstup spuštění tohoto kódu., Rozhodnutí hranici pro výcvikové sady vypadá takto:

Jak můžeme vidět a jak jsme se naučili v Tuning sekci Parametry, protože C má malou hodnotu proudu (0,1) rozhodovací hranice je hladký.
nyní, pokud zvýšíme C z 0.,1 až 100 budeme mít více křivek v rozhodovací hranice:

Co by se stalo, pokud budeme používat C=0.1 ale teď jsme zvýšení Gama od 0,1 do 10? Uvidíme!

Co se tady stalo? Proč máme tak špatný model?, Jak jste viděli v sekci Parametry ladění, vysoká gama znamená, že při výpočtu věrohodné hyperplane považujeme pouze body, které jsou blízké. Protože hustota zelené body je vysoká pouze ve vybraných zelené oblasti, v které oblasti body jsou dost blízko, aby věrohodně nadroviny, tak ty nadroviny byli vybráni. Buďte opatrní s gama parametr, protože to může mít velmi špatný vliv na výsledky modelu, je-li nastavena na velmi vysokou hodnotu (to, co je „velmi vysoká hodnota“ závisí na hustotě datových bodů).,
pro tento příklad jsou nejlepší hodnoty pro C a gama 1.0 a 1.0. Teď, když jsme se spustit náš model na test set dostaneme následující diagram:

A Zmatek Matice vypadá takto:

Jak můžete vidět, máme pouze 3 Falešně Pozitivních a pouze 4 Falešně Negativních., Přesnost tohoto modelu je 93%, což je opravdu dobrý výsledek, získali jsme lepší skóre než pomocí KNN (přesnost 80%).
poznámka: přesnost není jedinou metrikou používanou v ML a také není nejlepší metrikou pro vyhodnocení modelu, kvůli paradoxu přesnosti. Tuto metriku používáme pro jednoduchost, ale později v kapitole metriky pro vyhodnocení algoritmů AI budeme hovořit o paradoxu přesnosti a ukážu další velmi populární metriky používané v této oblasti.,
závěry
v tomto článku jsme viděli velmi populární a výkonný algoritmus učení pod dohledem, podpůrný vektorový stroj. Naučili jsme se základní myšlenku, co je hyperplane, co jsou podpůrné vektory a proč jsou tak důležité. Viděli jsme také spoustu vizuálních reprezentací, které nám pomohly lépe porozumět všem koncepcím.
dalším důležitým tématem, kterého jsme se dotkli, je trik jádra, který nám pomohl vyřešit nelineární problémy.
abychom měli lepší model, viděli jsme techniky pro vyladění algoritmu., Na konci článku jsme měli příklad kódu v Pythonu, který nám ukázal, jak můžeme použít algoritmus KNN.
Jako poslední myšlenky, bych chtěl dát nějaké výhody & nevýhody a některé populární případy použití.,
Klady
- SVN může být velmi efektivní, protože používá pouze podmnožinu trénovací data, pouze podpora vektorů
- Funguje velmi dobře na menší sady dat, na non-lineární datové sady a vysokou dimenzionální prostory
- Je velmi efektivní v případech, kdy počet rozměrů je větší než počet vzorků
- může mít vysoká přesnost, někdy může vykonávat i lepší než neuronové sítě
- velmi citlivé na overfitting
Zápory
- čas Tréninku je vysoká, když máme velkých datových souborů
- Když data set má více šumu (jsem.,e. cílové třídy jsou překrývající se) SVM nebude fungovat dobře
Populární Případy Použití
- Text Klasifikace
- Detekce spam
- analýza Sentimentu
- Aspekt-na základě uznání
- Aspekt-na základě uznání
- rozpoznávání Ručně psaného číslice
