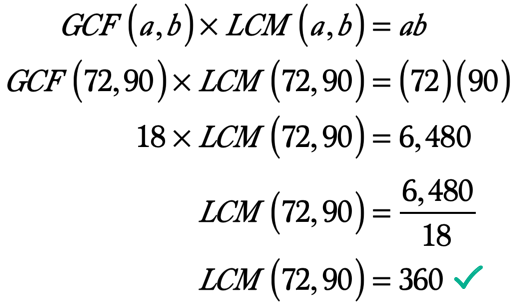Když se učíš, jak najít GCF a LCM dvou kladných čísel, jsi objevil velmi zajímavý vztah mezi dvěma veličinami?

udělal jsem to! Vlastně jsem to objevil náhodou, když jsem byl mladý student a myslel jsem, že jsem narazil na něco, co bylo „revoluční“. Byl jsem tak nadšený, že jsem to sdílel se svým učitelem., Ale k mé frustraci se na mě podíval do očí a řekl, že to už bylo osvědčené matematické prohlášení. Cítil jsem se na chvíli odradit, ale vrátil jsem se ke své školní práci a tlačil na.

Pokud jste se setkali to přesto, tam je pozoruhodný algebraické vztah nebo souvislost mezi Největší Společný Faktor (GCF) a Nejmenší Společný Násobek (LCM) dvou čísel. V této lekci jsou čísla, která chceme, ta, která patří pouze k souboru pozitivních celých čísel.,
níže je algebraické spojení mezi GCF a LCM dvou pozitivních celých čísel.
vzorec GCF-LCM
varování: opravdu neexistuje nic takového jako“GCF-LCM vzorec“. Jen jsem si vymyslel jméno pro snadnou orientaci. Můžete to nazvat cokoli chcete, pokud slouží svému účelu.,
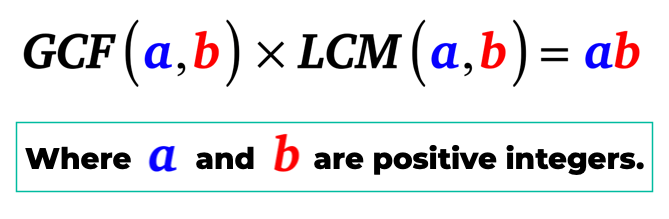
Jednoduše řečeno, největší společný dělitel a a b, když se násobí, aby nejmenší společný násobek čísel a a b je rovna součinu a a b. To je, a a b jsou kladná celá čísla.
Příklad Problémů
Příklad 1: GCF 12 a 16 je 4. Jaký je LCM 12 a 16?
LCM 12 a 16 můžete určit pomocí jedné ze dvou níže uvedených metod.,
- Nalezení LCM pomocí Seznamu Metoda
- Nalezení LCM pomocí prvočíselný Rozklad Metoda
Nicméně, tam je mnohem rychlejší způsob. Můžete využít „GCF-LCM vzorec“, protože znáte dvě celá čísla a jeho GCF. Stačí připojit hodnoty do vzorce a pak vyřešit pro LCM.
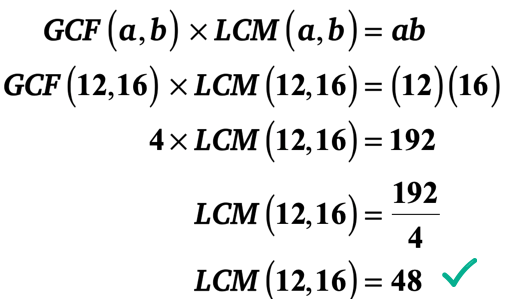
nechám to na vás, ověřte, že nejmenší společný násobek 12 a 16 je opravdu 48.
příklad 2: LCM 24 a 40 je 120. Jaký je GCF 24 a 40?,
tento problém je přesným opakem příkladu 1, protože místo GCF dostanete hodnotu LCM.
takže to jsou informace, které známe. Pojďme je rozdělit pro přehlednost.
▶︎ LCM(24,40) = 120
▶︎ a=24 a b=40 proto ab = \left( {24} \right)\left( {40} \right) = 960
📌 Poznámka: To nezáleží na tom, která čísla jsou a a b. To nic nezmění na výsledku konečnou odpověď. Je však dobré standardizovat vaše řešení. Navrhuji, abyste nechat být menší celé číslo, zatímco b být větší celé číslo.,
nahraďte známé hodnoty do vzorce a poté vyřešte pro GCF 24 a 40.
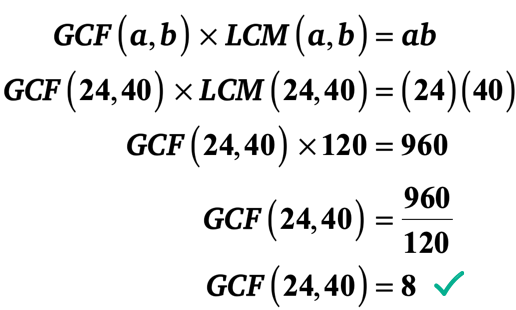
Příklad 3: Najděte na GCF 20 a 25 tím, že první výpočet nejmenší společný násobek 20 a 25.
tento problém se bude trochu lišit od příkladů #1 a # 2. Budete muset nejprve vypočítat nejméně obyčejný násobek (LCM) 20 a 25. Poté můžete vyřešit největší společný faktor (GCF) 20 a 25 pomocí vzorce GCF-LCM.
tak jdeme na to!, Chcete-li najít LCM 20 a 25, napíšeme prvních několik násobků 20 a 25. První společný násobek, který se objeví, bude náš LCM.
Násobky 20: 20, 40, 60, 80, 100, 120
Násobky 25: 25, 50, 75, 100, 125, 150
Protože číslo 100 se objeví jako první společný násobek čísel 20 a 25, pak můžeme tvrdit, že nejmenší společný násobek 20 a 25 je 100.
nyní máme všechny informace k použití vzorce. Níže jsou hodnoty, které hodláme nahradit do vzorce pro řešení LCM 20 a 25.,
◉ výrobku a a b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ nejmenší společný násobek 20 a 25 → LCM\left( {20,25} \right) = 100
Zde je výpočet, jak vyřešit na GCF 20 a 25:
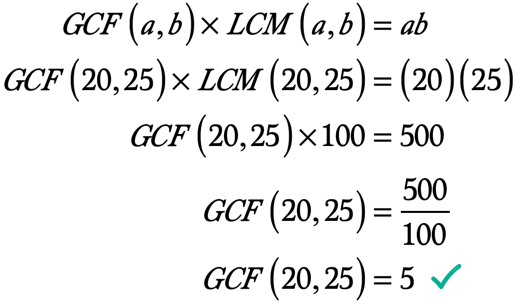
Příklad 4: Najděte nejmenší společný násobek 63 a 84 o první výpočet GCF 63 a 84.
tento problém je velmi podobný příkladu #3. Jediný rozdíl spočívá v tom, že nejprve vypočítáte GCF namísto LCM, podle pokynů samotného problému.,
pojďme najít všechny faktory 63 a 84. Můžete použít techniku „Rainbow method“ pro faktor daných celých čísel.
Všimněte si, že největší nebo nejvyšší společný faktor mezi oběma seznamy je 21.
Faktory 63: 1, 3, 7, 9, 21, 63
Faktory 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Proto, Největší Společný Faktor, 63 a 84 je 21. Takže GCF \ left ({63,84} \right) = 21.,
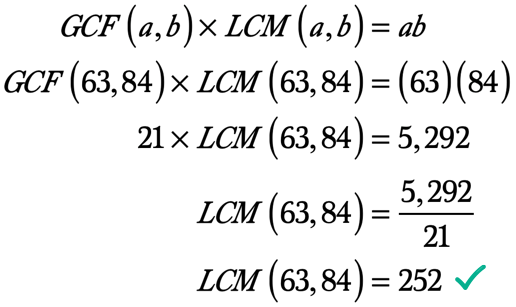
Příklad 5: Najděte nejmenší společný násobek 72 a 90 pomocí GCF-LCM Vzorec.
jak již víme, můžeme najít LCM dvou celých čísel s hodnotou jeho GCF pomocí vzorce GCF-LCM.,
Výpis oba faktory, 72 a 90, máme:
Všechny faktory 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Všechny faktory 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Když jsme se porovnat seznamy faktorů, vidíme, že 18 je faktor, který je společný pro oba ale má největší nebo největší hodnotu. Znamená to, že GCF 72 a 90 je 18, tedy GCF \ left ({72,90} \right) = 18.
nyní jsme připraveni nahradit hodnoty níže ve vzorci.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Zde je výpočet, jak najít nejmenší společný násobek vzhledem k tomu, že už víme, GCF z dvou celých čísel a jejich produktu.