la forma más fácil de capturar la idea de una población en crecimiento es con un organismo unicelular, como una bacteria o un ciliado. En la Figura 1, se muestra una población de paramecio en un pequeño portaobjetos de depresión de laboratorio. En esta población los individuos se dividen una vez al día. Por lo tanto, a partir de un solo individuo en el día 0, esperamos, en días sucesivos, 2, 4, 8, 16, 32, y 64 individuos en la población., Podemos ver aquí que, en cualquier día en particular, el número de individuos en la población es simplemente el doble de lo que el número era el día anterior, por lo que el número de hoy, llámelo N(Hoy), es igual al doble del número de ayer, llámelo N(ayer), que podemos escribir de forma más compacta como N(hoy) = 2N(ayer).
así que tiene sentido escribir esto como, N ( t) = 2N(t – 1) donde t podría tomar cualquier valor en absoluto.,
ahora podemos generalizar esta idea un poco si observamos que en el día seis el número es igual al doble del número en el día cinco, o N ( 6) = 2N(5) y en el día cinco el número es igual al doble del número en el día cuatro, o N(5) = 2n(4), etc.
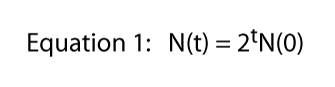
donde t es para cualquier momento en absoluto (por ejemplo, si t = 6, N(6) = 26).
finalmente observamos que esta ecuación se derivó de la situación específica mostrada en la Figura 1, donde una división por día fue la regla dura y rápida., De ahí es de donde viene el 2 en la ecuación 1 — de cada paramecio individual obtenemos dos individuos al día siguiente. Por supuesto, la tasa de división podría ser cualquier cosa. Si hubiera dos divisiones por día pero una célula siempre muriera, esperaríamos tres individuos de cada individuo y la ecuación 1 sería N ( t) = 3TN(0)., Por lo tanto, la tasa de división podría ser cualquier número y la ecuación general se convierte en,
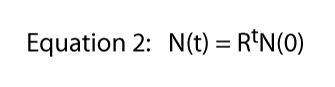
donde R Generalmente se llama la tasa finita de aumento de la población (en el caso real de dividir el paramecio tasa finita de aumento de la población es igual a la tasa de división). En la Figura 2 ilustramos esta ecuación para varios valores de R. normalmente se conoce como la ecuación exponencial, y la forma de los datos en la Figura 2 es la forma general llamada exponencial.,
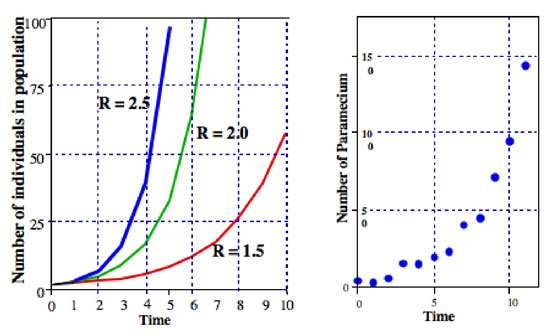
Cualquier valor de R puede ser representada en un número infinito de maneras (por ejemplo, si R = 16, podemos escribir R = 8 x 2, o R = 42, o R = 32/2, o R = 2.718282.77). Esa última expresión (R = 2.718282.,77) hace uso de una constante importante que podría ser recordada del cálculo elemental, la constante de Euler. Expresar cualquier valor de R como la constante de Euler elevada a alguna potencia es realmente extremadamente útil-trae toda la potencia del cálculo a la imagen.,olize la constante de Euler como e podemos escribir la ecuación 2 como
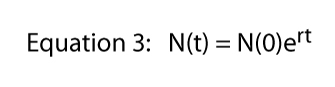
ahora si tomamos el logaritmo natural de ambos lados de la ecuación 3 — recuerde Ln(ex) = X — ecuación 3 se convierte en: LN = LN + RT
y si comenzamos la población con un solo individuo (como en el ejemplo anterior), tenemos

de lo que vemos que el logaritmo natural de la población, en cualquier momento en particular, es una constante, veces ese tiempo., La constante r se conoce como la tasa intrínseca de aumento natural (figura 2).
todo tipo de microorganismos exhiben patrones que están muy cerca del crecimiento exponencial de la población. Por ejemplo, en el gráfico de la derecha de la Figura 2 hay una población de paramecio que crece en un cultivo de laboratorio. El patrón de crecimiento es muy cercano al patrón de la ecuación exponencial.
otra forma de escribir la ecuación exponencial es como una ecuación diferencial, es decir, representando el crecimiento de la población en su forma dinámica., En lugar de preguntar cuál es el tamaño de la población en el tiempo t, preguntamos cuál es la tasa a la que la población está creciendo en el tiempo t. la tasa se simboliza como dN/dt que simplemente significa «cambio en N relativo al cambio en t», y si recuerda su cálculo básico, podemos encontrar la tasa de crecimiento diferenciando la ecuación 4, que nos da
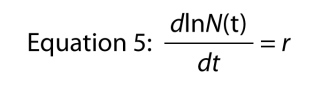
que es algo notable, porque dice que la tasa de crecimiento del registro del número en la población es constante., Esa tasa constante de crecimiento del tronco de la población es la tasa intrínseca de aumento.,
Recordemos que la tasa de cambio del logaritmo de un número es el mismo como el «per cápita» cambio en el número que, lo que significa que podemos escribir la Ecuación 5 como

cuando se omite la variable t, ya que es obvio a donde va, y luego nos reorganizar un poco para llegar con
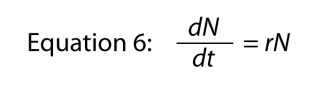
donde el parámetro r es, de nuevo, la tasa intrínseca de incremento natural., La relación básica entre la tasa finita de aumento y la tasa intrínseca es
r = ln(R)
donde LN se refiere al logaritmo natural. Tenga en cuenta que la ecuación 6 y la ecuación 3 son solo formas diferentes de la misma ecuación (la ecuación 3 es la forma integrada de la ecuación 6; La ecuación 6 es la forma diferenciada de la ecuación 3), y ambas pueden ser referidas simplemente como la ecuación exponencial.,

La ecuación exponencial es un modelo útil de simple poblaciones, al menos por períodos de tiempo relativamente cortos., Por ejemplo, si un técnico de laboratorio necesita saber cuándo un cultivo bacteriano alcanza una cierta densidad de población, la ecuación exponencial se puede utilizar para proporcionar una predicción de cuándo exactamente se alcanzará ese tamaño de población. Otro ejemplo es el caso de las plagas agrícolas. Los herbívoros son siempre problemas potencialmente importantes para las plantas. Cuando las plantas sometidas a tales brotes son agrícolas, es decir, cultivos, la pérdida puede ser muy significativa tanto para el agricultor como para el consumidor. Por lo tanto, siempre hay presión para evitar tales brotes., Desde la Segunda Guerra Mundial, la principal arma en la lucha contra estos brotes de plagas han sido los pesticidas químicos, como el DDT. Sin embargo, en los últimos años nos hemos dado cuenta de que estos pesticidas son extremadamente peligrosos a largo plazo, tanto para el medio ambiente como para las personas. En consecuencia, ha habido un movimiento para limitar la cantidad de pesticidas que se rocían para combatir las plagas. La forma principal de hacerlo es establecer un umbral económico, que es la densidad de población de la plaga potencial por debajo de la cual el daño al cultivo es insignificante (es decir, no es realmente necesario rociar)., Cuando la población de plagas aumenta por encima de ese umbral, el agricultor necesita tomar medidas y aplicar algún tipo de pesticida u otros medios para controlar la plaga. Dada la naturaleza de este problema, a veces es de suma importancia poder predecir cuándo la plaga alcanzará el umbral económico. Conocer la R para la especie de plaga permite al agricultor predecir cuándo será necesario aplicar algún tipo de procedimiento de control (Figura 3).
la ecuación exponencial también es un modelo útil para desarrollar ideas intuitivas sobre las poblaciones., El ejemplo clásico es un estanque con una población de nenúfares. Si cada Nenúfar se reproduce a sí mismo (dos Nenúfar toman el lugar de donde había estado una) cada mes, y tomó, digamos, tres años para que el estanque se llenara a medio llenar con Nenúfar, ¿cuánto tiempo más tomará para que el estanque esté completamente cubierto con Nenúfar? Si no se detiene a pensar con demasiada claridad, es tentador decir que tomará tanto tiempo, tres años, para que la segunda mitad del estanque se llene tanto como la primera. La respuesta, por supuesto, es un mes.,
otro ejemplo popular es el proverbial matemático egipcio antiguo (o a veces persa) que pide el pago del Rey en forma de granos de trigo (a veces arroz). Un grano en el primer cuadrado de un tablero de ajedrez, dos granos en el segundo cuadrado, y así sucesivamente, hasta el último cuadrado. El Faraón no puede imaginar que un pago tan simple podría ascender a mucho, y así está de acuerdo. Pero no apreció plenamente el crecimiento exponencial., Dado que hay 64 casillas en el tablero de ajedrez, podemos usar la ecuación 2 para determinar cuántos granos de trigo se requerirán para pagar en el último cuadrado (R elevado a la potencia 64, que es aproximadamente 18,446,744,074,000,000,000 — una gran cantidad de trigo, ciertamente más que en todo el Reino). Estos ejemplos enfatizan la forma frecuentemente sorprendente en que un proceso exponencial puede conducir a números muy grandes muy rápidamente.
