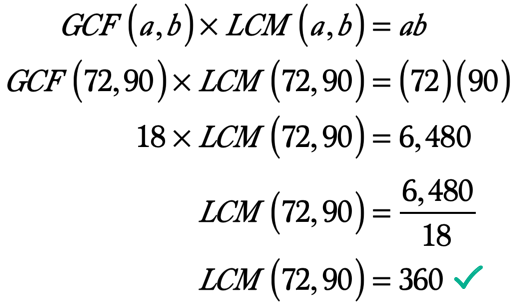cuando estudiaba cómo encontrar el GCF y LCM de dos números positivos, ¿descubrió una relación muy interesante entre las dos cantidades?

yo lo hice! En realidad lo descubrí por accidente cuando era un joven estudiante y pensé que me topé con algo que era «revolucionario». Estaba tan emocionada que lo compartí con mi maestra., Pero para mi frustración, me miró a los ojos y dijo que ya era una declaración matemática probada. Me sentí desanimada por un momento, pero volví a mi trabajo escolar y seguí adelante.

Si aún no lo ha encontrado, hay una notable relación algebraica o vínculo entre el mayor Factor común (GCF) y el mínimo común múltiple (LCM) de dos números. En esta lección, los números que queremos son los que pertenecen al conjunto de enteros positivos solamente.,
a continuación se muestra la conexión algebraica entre el GCF y el LCM de dos enteros positivos.
la fórmula GCF-LCM
advertencia: realmente no hay tal cosa como la»fórmula GCF-LCM». Acabo de inventar el nombre para facilitar la referencia. Puedes llamarlo como quieras, siempre y cuando sirva a su propósito.,
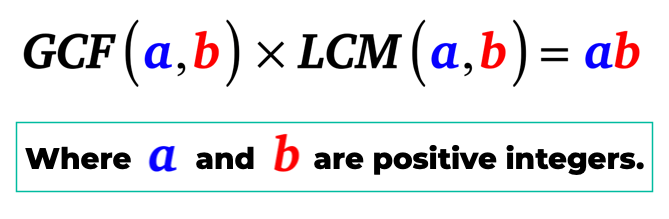
Simplemente, el máximo común divisor de a y b cuando se multiplica para el mínimo común múltiplo de a y b es igual al producto de a y b. Es decir, a y b son enteros positivos.
Problemas de Ejemplo
Ejemplo 1: El MCD de 12 y 16 es 4. ¿Qué es el LCM de 12 y 16?
Puede determinar el LCM de 12 y 16 utilizando cualquiera de los dos métodos a continuación.,
- encontrar LCM usando el método de Lista
- encontrar LCM usando el método de factorización Prime
Sin embargo, hay una forma mucho más rápida. Puede aprovechar la «fórmula GCF-LCM» porque conoce los dos enteros y su GCF. Simplemente conecte los valores en la fórmula y luego resuelva para el LCM.
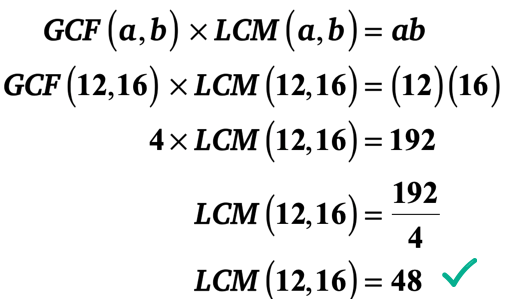
yo se lo dejo a usted para verificar que el MCM de 12 y 16 años es, de hecho, 48.
Ejemplo 2: El LCM de 24 y 40 es 120. ¿Qué es el GCF de 24 y 40?,
Este problema es exactamente lo contrario del Ejemplo 1 porque se le da el valor del LCM en lugar del GCF.
así que esta es la información que conocemos. Vamos a detallarlos para mayor claridad.
▶ L LCM (24,40) = 120
▶ a a=24 y B=40 por lo tanto ab = \left ({24} \right)\left ({40} \right) = 960
Note Nota: realmente no importa qué números son a y b. no cambiará el resultado de la respuesta final. Sin embargo, es una buena práctica estandarizar su solución. Sugiero que deje que a sea el entero más pequeño mientras que b sea el entero más grande.,
sustituyamos los valores conocidos en la fórmula y luego resolvamos el GCF de 24 y 40.
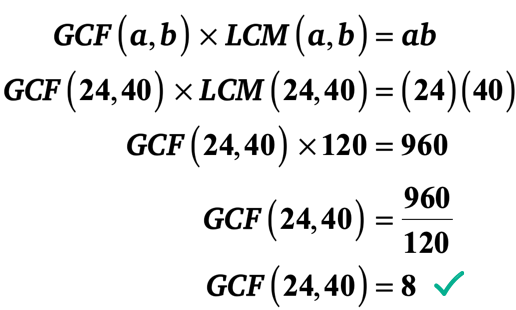
Ejemplo 3: Hallar el MCD de 20 y 25 por primera calcular el MCM de 20 y 25.
Este problema será un poco diferente de los ejemplos #1 y #2. Tendrá que calcular primero el mínimo común múltiplo (LCM) de 20 y 25. Después de eso, puede resolver el mayor factor común (GCF) de 20 y 25 utilizando la fórmula GCF-LCM.
Así que aquí vamos!, Para encontrar el LCM de 20 y 25, escribiremos los primeros múltiplos de 20 y 25. El primer múltiplo común que aparece será nuestro LCM.
Múltiplos de 20: 20, 40, 60, 80, 100, 120
Múltiplos de 25: 25, 50, 75, 100, 125, 150
Desde el número 100 se muestra como el primer múltiplo común de 20 y 25, entonces podemos afirmar que el LCM 20 y 25 años es de 100.
Ahora tenemos toda la información para usar la fórmula. A continuación se presentan los valores que vamos a sustituir en la fórmula para resolver para el LCM de 20 y 25.,
l producto de A y B → ab = \left( {20} \right)\left( {25} \right) = 500
The El LCM de 20 y 25 → LCM\left( {20,25} \right) = 100
Aquí está el cálculo a resolver para el GCF de 20 y 25:
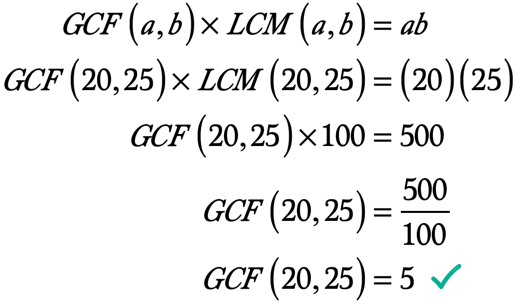
Ejemplo 4: encuentre el LCM de 63 y 84 calculando primero el GCF de 63 y 84.
Este problema es muy similar al Ejemplo # 3. La única diferencia es que calculará primero el GCF en lugar del LCM, según lo indicado por el problema en sí.,
vamos a encontrar todos los factores de 63 y 84. Puede utilizar la técnica «método arco iris» para factorizar los enteros dados.
observe que el factor común más grande o más alto entre las dos listas es 21.
Factores de 63: 1, 3, 7, 9, 21, 63
Factores de 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
por lo Tanto, el máximo Factor Común de 63 y 84 es de 21 años. Por lo tanto, GCF\left( {63,84} \right) = 21.,
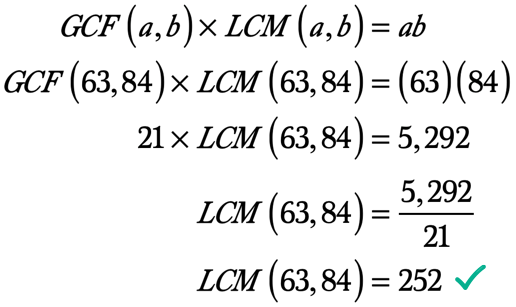
Ejemplo 5: Hallar el MCM de 72 y 90 con el GCF-LCM Fórmula.
como ya sabemos, podemos encontrar el LCM de dos enteros con el valor de su GCF usando la fórmula GCF-LCM.,
Listado tanto, los factores de 72 y 90, tenemos:
Todos los factores de 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Todos los factores de 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Cuando comparamos las listas de factores, vemos que el 18 es el factor que es común a ambos, pero tiene el más grande o de mayor valor. Significa que el GCF de 72 y 90 ES 18, es decir, GCF\left ({72,90} \ right) = 18.
Ahora estamos listos para sustituir los valores a continuación en la fórmula.,
ab ab = \ left ({72} \right)\left ({90} \right) = 6,480
G GCF\left ({72,90} \right) = 18
Aquí está el cálculo para encontrar el LCM dado que ya conocemos el GCF de los dos enteros y su producto.