coeficiente de correlación
¿Qué tan bien representa realmente su ecuación de regresión
su conjunto de datos?una de las formas de determinar la respuesta a esta pregunta es examinar el coeficiente de correlación y el coeficiente de determinación.,
|
|
El coeficiente de correlación, r, y |
además de aparecer con la información de regresión, los valores rand r 2 se pueden encontrar debajo de las barras, #5 Statistics → EQ #7 r y #8 R 2 .,
el Coeficiente de Correlación, r :
la dirección de una relación lineal entre dos variables. El coeficiente de correlación lineal
a veces se conoce como el coeficiente de correlación del momento del producto de Pearson en honor de su desarrollador Karl Pearson.
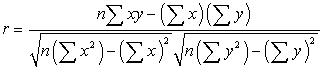
donde n es el número de pares de datos.,
(¿no te alegras de tener una calculadora gráfica que calcula esta fórmula?)
y correlaciones lineales negativas, respectivamente.
a +1. Un valor de r de exactamente +1 indica un ajuste positivo Perfecto., Los valores positivos
indican una relación entre las variables x E y tal que a medida que los valores para X aumentan, los valores para y también aumentan.
a -1. Un valor de R de exactamente -1 indica un ajuste negativo perfecto. Los valores negativos
indican una relación entre x E y tal que como los valores para X aumentan, los valores
PARA y disminuyen.
cerca de 0., Un valor cercano a cero significa que hay una relación aleatoria, no lineal
entre las dos variables
empleadas.
. Si r = +1, la pendiente de esta línea es positiva. Si r = -1, la pendiente de esta línea
es negativa.
menor que 0.,5 se describe generalmente como débil. Estos valores pueden variar en función del»tipo» de datos que se examina. Un estudio que utiliza datos científicos puede requerir una correlación más fuerte que un estudio que utiliza datos de Ciencias Sociales.
Coeficiente de Determinación, r 2 o R2 :
la varianza (fluctuación) de una variable que es predecible a partir de la otra variable.,
Es una medida que nos permite determinar cómo puede ser cierto al hacer predicciones a partir de un determinado modelo / gráfico.
de la asociación lineal entre x y y.,
a la línea de mejor ajuste. Por ejemplo, si r = 0.922, entonces r 2 = 0.850, lo que significa que
85% de la variación total iny puede explicarse por la relación lineal entre x
E y (como se describe en la ecuación de regresión). El otro 15% de la variación total
En y permanece inexplicable.
representa los datos., Si la línea de regresión pasa exactamente a través de cada punto en el gráfico de dispersión
, sería capaz de explicar toda la variación. Cuanto más lejos está la línea de los puntos, menos es capaz de explicar.

