Después de la construcción de una máquina modelo de aprendizaje, el siguiente paso es evaluar el desempeño del modelo y entender cómo de buena es nuestro modelo está en contra de un modelo de referencia., La métrica de evaluación que se utilizará dependerá del tipo de problema que esté tratando de resolver, ya sea un problema supervisado o no supervisado, y si se trata de una tarea de clasificación o regresión.
en este post voy a hablar de dos importantes métricas de evaluación utilizadas para los problemas de regresión y destacar la diferencia clave entre ellos.
R-cuadrado, también conocido como la determinación del coeficiente, define el grado en que la varianza en la variable dependiente (o objetivo) puede ser explicada por la variable independiente (características).,
entendamos esto con un ejemplo-digamos que el valor R-cuadrado para un modelo en particular resulta ser 0.7. Esto significa que el 70% de la variación en la variable dependiente se explica por las variables independientes.
idealmente, nos gustaría que las variables independientes sean capaces de explicar toda la variación en la variable objetivo. En ese escenario, el valor de R al cuadrado sería 1. Así podemos decir que más alto el valor R-cuadrado, mejor en el modelo.,
así que, en términos simples, mayor es la r al cuadrado, más variación se explica por sus variables de entrada y por lo tanto mejor es su modelo. Además, el R-cuadrado variaría de 0 a 1. Aquí está la fórmula para calcular R-cuadrado –
El R-cuadrado se calcula dividiendo la suma de cuadrados de residuos del modelo de regresión (dado por SSres) por la suma total de cuadrados de errores del modelo promedio (dado por SStot) y luego restarlo de 1.,
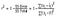
Uno de los inconvenientes de r-cuadrado es que asume cada una de las variables ayuda en la explicación de la variación en el destino, que no siempre puede ser cierto. Por ejemplo, si agregamos nuevas características a los datos (que pueden o no ser útiles), el valor R-cuadrado para el modelo aumentaría o permanecería igual, pero nunca disminuiría.
esto es atendido por una versión ligeramente modificada de r-cuadrado, llamada R-cuadrado ajustado.,
R-cuadrado ajustado
Similar a R-cuadrado, el R-cuadrado ajustado mide la variación en la variable dependiente (o objetivo), explicada solo por las características que son útiles para hacer predicciones. A diferencia de R-cuadrado, el R-cuadrado ajustado lo penalizaría por agregar características que no son útiles para predecir el objetivo.
vamos a entender matemáticamente cómo esta característica se acomoda en R-cuadrado ajustado., Aquí está la fórmula para ajustar r-cuadrado

Aquí R^2 es el r-cuadrado calculado, N es el número de filas y M es el número de columnas. A medida que aumenta el número de entidades, el valor en el denominador disminuye.
- si el R2 aumenta por un valor significativo, entonces el R-cuadrado ajustado aumentaría.
- si no hay un cambio significativo en R2, entonces el R2 AJUSTADO disminuiría.
