secuencia
una secuencia es un conjunto de cosas (generalmente números) que están en orden.
progresiones Geométricas
En una progresión Geométrica de cada término se encuentra multiplicando el término anterior por una constante.
en General escribimos una secuencia geométrica como esta:
{a, ar, ar2, ar3, …, }
donde:
- a es el primer término, y
- r es el factor entre los términos (que se llama la «razón común»)
Pero cuidado, r no debe ser 0:
- Cuando r=0, obtenemos la secuencia {a,0,0,…} que no es geométrico
La regla
También podemos calcular cualquier término usando la regla:
xn = ar(n-1)
(usamos «n-1» porque ar0 es para el 1er término)
una secuencia geométrica también puede tener valores cada vez más pequeños:
ejemplo:
4, 2, 1, 0.5, 0.25, …,
Esta secuencia tiene un factor de 0.5 (la mitad) entre cada número.
Su regla es xn = 4 × (0.5)n-1
¿por qué la secuencia «geométrica»?,
porque es como aumentar las dimensiones en Geometría:
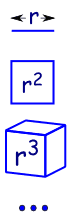 |
una línea es 1-dimensional y tiene una longitud de r |
| en 2 dimensiones un cuadrado tiene un área de R2 | |
| en 3 dimensiones un cubo tiene volumen R3 | |
| etc (Sí podemos tener 4 y más dimensiones en matemáticas)., |
Las secuencias geométricas a veces se llaman progresiones geométricas (G. P.’s)
sumando una serie geométrica
para sumar estos:
a + ar + ar2 + … + ar(n-1)
(cada término es ark, donde k comienza en 0 y sube a n-1)
Podemos usar esta práctica fórmula:

a es el primer término
R es la «relación común» entre términos
n es el número de términos
¿Cuál es ese divertido símbolo Σ?, Se llama Notación Sigma
| (llamado Sigma) significa «suma» |
Y por debajo y por encima de ella se muestra el inicio y final de los valores:
Se dice que «la Suma de hasta n, donde n va de 1 a 4. Respuesta=10
La fórmula es fácil de usar …, simplemente «enchufa» los valores de A, R y n
usando la fórmula
veamos la fórmula en acción:
ejemplo: granos de arroz en un tablero de Ajedrez

en la página dígitos binarios damos una Ejemplo de granos de arroz en un tablero de ajedrez. La pregunta es:
cuando colocamos arroz en un tablero de ajedrez:
- 1 grano en el primer cuadrado,
- 2 granos en el segundo cuadrado,
- 4 granos en el tercero y así sucesivamente,
- …
… doblar los granos de arroz en cada cuadrado …
…, cuántos granos de arroz en total?
así que tenemos:
- a = 1 (el primer término)
- r = 2 (dobles cada vez)
- n = 64 (64 casillas en un tablero de ajedrez)
así:

se convierte en:
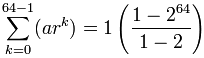
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
que fue exactamente el resultado que obtuvimos en la página de dígitos binarios (¡gracias a Dios!)
y otro ejemplo, esta vez con r menos de 1:
¿por qué funciona la fórmula?,
veamos por qué funciona la fórmula, porque llegamos a usar un «truco» interesante que vale la pena conocer.
¿nota que S y S·r son similares?
ahora restarlos!
Wow! Todos los Términos en el medio se cancelan cuidadosamente.,
(Que es un truco)
restando S·r de S obtenemos un simple resultado:
S − S·r = a − arn
Vamos a reordenar a encontrar S:
Que es nuestra fórmula (ta-da!):

serie geométrica infinita
entonces, ¿qué sucede cuando n va al infinito?,
podemos usar esta fórmula:
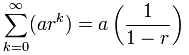
Pero cuidado:
r debe estar entre (pero sin incluir) -1 y 1
y r no debe ser 0 porque la secuencia {a,0,0,…} no es geométrico
así que nuestra serie geométrica infnite tiene una suma finita cuando la relación es menor que 1 (y mayor que -1)
vamos a traer de vuelta nuestro ejemplo anterior, y ver lo que sucede:
|
Basta con mirar este cuadrado: sumando 12 + 14 + 18 + … ¡terminamos con todo!, |
 |
Recurrentes Decimal
En otra página nos preguntó «¿0.999… igual a 1?», Bueno, veamos si podemos calcularlo:



