respuesta rápida:
para un triángulo en ángulo recto:

la función sinusoidal toma el ángulo θ y da la relación opuesta hipotenusa
la función sinusoidal inversa sin-1 toma la relación oppositehypotenuse y da el ángulo θ
y el coseno y la tangente siguen una idea similar.,
y ahora para los detalles:
seno, coseno y tangente se basan en un triángulo en ángulo recto
son funciones muy similares … así que vamos a mirar la función seno y luego seno inverso para aprender de qué se trata.,
Función Seno
El Seno del ángulo θ es:
- la longitud del lado Opuesto al ángulo θ
- dividido por la longitud de la Hipotenusa
O, más sencillamente:
sen(θ) = Opuesto / Hipotenusa
La Función Seno nos puede ayudar a resolver cosas como esto:
Inversa de la Función Seno
Pero a veces es el ángulo que necesitamos encontrar.
Aquí es donde entra «seno inverso».
responde a la pregunta » ¿qué ángulo tiene seno igual a opuesto / hipotenusa?,»
el símbolo para el seno inverso es sin-1, o a veces arcsin.
Son Como hacia Adelante y hacia Atrás!

- sin toma un ángulo y nos da la relación»opuesto/hipotenusa «
- sin-1 toma la relación» opuesto/hipotenusa » y nos da el ángulo.
ejemplo:
Calculadora
 |
En la calculadora, pulse uno de los siguientes (dependiendo de la marca de su calculadora):o ‘2ndF pecado’ o ‘cambio de pecado’. |
en su calculadora, intente usar sin y luego sin-1 para ver qué sucede
¡más de un ángulo!
el seno inverso solo muestra un ángulo … pero hay más ángulos que podrían funcionar.
ejemplo: aquí hay dos ángulos donde opuesto / hipotenusa = 0.,5
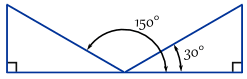
De hecho, hay infinitamente muchos ángulos, porque se pueden seguir sumando (o restando) 360°:
Recuerda esto, porque hay veces cuando usted realmente necesita uno de los otros ángulos!
Resumen
El Seno del ángulo θ es:
sen(θ) = Opuesto / Hipotenusa
Y Seno Inverso es :
sin-1 (Opuesto / Hipotenusa) = θ
¿Qué Acerca de «cos» y «tan» … ?
exactamente la misma idea, pero diferentes relaciones laterales.,
Coseno
El Coseno de un ángulo θ es:
cos(θ) = Adyacente / Hipotenusa
Y Coseno Inverso es :
cos-1 (Adyacente / Hipotenusa) = θ
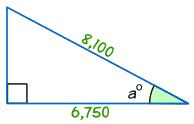
Ejemplo: Encontrar el tamaño de un ángulo de°
cos a° = Adyacente / Hipotenusa
cos a° = 6,750/8,100 = 0.8333…
a° = cos – 1 (0,8333…) = 33.,6° (a 1 decimal)
Tangente
La Tangente de un ángulo θ es:
tan(θ) = Opuesto / Adyacente
de Modo Inverso de la Tangente es :
tan-1 (Opuesto / Adyacente) = θ
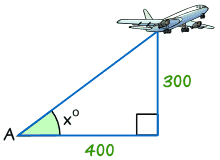
Ejemplo: Encontrar el valor del ángulo x°
tan x° = Opuesto / Adyacente
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (correcto a 1 decimal)
Otros nombres
a veces sin-1 se llama asin o arcsin
Asimismo cos-1 se llama acos o arccos
y tan-1 se llama atan o arctan
ejemplos:
- arcsin(y) es lo mismo que sin-1(y)
- atan(θ) es lo mismo que tan-1(θ)
- etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- Pero el seno inverso y el coseno inverso no «continúan para siempre» como lo hacen el seno y el coseno …
veamos el ejemplo del Coseno.
Aquí está el coseno y el coseno inverso trazados en el mismo gráfico:

coseno y coseno inverso
son imágenes espejo (sobre la diagonal)
pero ¿por qué el coseno inverso se corta en la parte superior e inferior (los puntos no son realmente parte de la función) … ?
porque ser una función solo puede dar una respuesta
cuando preguntamos » ¿qué es cos-1 (x) ?,»
una respuesta o infinitamente muchas respuestas
pero vimos anteriormente que hay infinitamente muchas respuestas, y la línea de puntos en el gráfico muestra esto.
así que sí, hay infinitas respuestas …
… pero imagina que escribes 0.5 en tu calculadora, presionas cos-1 y te da una lista interminable de posibles respuestas …
así que tenemos esta regla de que una función solo puede dar una respuesta.
por lo tanto, al cortarlo así obtenemos solo una respuesta, pero debemos recordar que podría haber otras respuestas.,
tangente y tangente inversa
y aquí está la función tangente y tangente inversa. Puedes ver cómo son imágenes especulares (sobre la diagonal) …?

Tangente

Tangente Inversa


