
En este artículo, usted aprenderá acerca de la SVM o Máquina de Soporte Vectorial, que es uno de los más populares algoritmos (es uno de los 10 mejores algoritmos) y sobre el Kernel Truco, que se ocupa de la no-linealidad y dimensiones superiores., Tocaremos temas como hiperplanos, multiplicadores de Lagrange, tendremos ejemplos visuales y ejemplos de código (similar al ejemplo de código utilizado en el capítulo KNN) para comprender mejor este algoritmo tan importante.
SVM Explained
La Máquina vectorial de soporte es un algoritmo de aprendizaje supervisado utilizado principalmente para la clasificación, pero también se puede usar para la regresión. La idea principal es que basado en los datos Etiquetados (datos de entrenamiento) el algoritmo trata de encontrar el hiperplano óptimo que se puede utilizar para clasificar nuevos puntos de datos. En dos dimensiones el hiperplano es una línea simple.,
Por lo general, un algoritmo de aprendizaje intenta aprender las características más comunes (lo que diferencia a una clase de otra) de una clase y la clasificación se basa en las características representativas aprendidas (por lo que la clasificación se basa en las diferencias entre clases). El SVM funciona al revés. Encuentra los ejemplos más similares entre clases. Esos serán los vectores de soporte.
como ejemplo, consideremos dos clases, manzanas y limones.,
otros algoritmos aprenderán las características más evidentes y más representativas de las manzanas y los limones, como las manzanas son verdes y redondeadas, mientras que los limones son amarillos y tienen forma elíptica.
en contraste, SVM buscará manzanas que son muy similares a los limones, por ejemplo, manzanas que son amarillas y tienen forma elíptica. Este será un vector de soporte. El otro vector de soporte será un limón similar a una manzana (verde y redondeado). Así que otros algoritmos aprenden las diferencias mientras que SVM aprende similitudes.,
Si visualizamos el ejemplo anterior en 2D, tendremos algo como esto:

a Medida que avanzamos de izquierda a derecha, todos los ejemplos serán clasificados como manzanas hasta llegar a la manzana amarilla. A partir de este punto, la confianza de que un nuevo ejemplo es una manzana disminuye mientras que la confianza de la clase limón aumenta., Cuando la confianza de la clase limón se vuelve mayor que la confianza de la clase manzana, los nuevos ejemplos se clasificarán como limones (en algún lugar entre la manzana amarilla y el limón verde).
basado en estos vectores de soporte, el algoritmo intenta encontrar el mejor hiperplano que separa las clases. En 2D la hyperplane es una línea, por lo que se vería así:

Aceptar pero, ¿por qué me llaman el azul de límite como en la imagen de arriba?, Yo también podría establecer límites como esta:

Como puede ver, tenemos un número infinito de posibilidades para dibujar la decisión de la frontera. Entonces, ¿cómo podemos encontrar el óptimo?
encontrar el hiperplano óptimo
intuitivamente la mejor línea es la línea que está lejos de los ejemplos de apple y lemon (tiene el margen más grande)., Para tener una solución óptima, tenemos que maximizar el margen en ambos sentidos (si tenemos varias clases, entonces tenemos que maximizarlo teniendo en cuenta cada una de las clases).

Así que si comparamos la imagen de arriba con la imagen de abajo, podemos observar fácilmente, que la primera es la óptima hyperplane (línea) y el segundo es un sub-óptimo de la solución, porque el margen es mucho menor.,

Porque lo que queremos es maximizar los márgenes de tomar en consideración todas las clases, en lugar de utilizar un margen para cada clase, se utiliza un «global» de margen, que toma en consideración todas las clases., Este margen se vería de la línea púrpura en la siguiente imagen:

Este margen es ortogonal a la línea de frontera y equidistante a los de soporte de vectores.
entonces, ¿dónde tenemos vectores? Cada uno de los cálculos (calcular distancia e hiperplanos óptimos) se realizan en espacio vectorial, por lo que cada punto de datos se considera un vector. La dimensión del espacio se define por el número de atributos de los ejemplos., Para entender las matemáticas detrás, por favor lea esta breve descripción matemática de vectores, hiperplanos y optimizaciones: SVM sucintamente.
En general, los vectores de soporte son puntos de datos que definen la posición y el margen del hiperplano. Los llamamos vectores de «soporte», porque estos son los puntos de datos representativos de las clases, si movemos uno de ellos, la posición y/o el margen cambiarán. Mover otros puntos de datos no tendrá efecto sobre el margen o la posición del hiperplano.,
para hacer clasificaciones, no necesitamos todos los puntos de datos de entrenamiento( como en el caso de KNN), tenemos que guardar solo los vectores de soporte. En el peor de los casos, todos los puntos serán vectores de soporte, pero esto es muy raro y si sucede, entonces debe verificar su modelo en busca de errores o errores.
así que básicamente el aprendizaje es equivalente a encontrar el hiperplano con el mejor margen, por lo que es un simple problema de optimización.,/h2>
los pasos básicos del SVM son:
- seleccione dos hiperplanos (en 2D) que separen los datos sin puntos entre ellos (líneas rojas)
- maximizar su distancia (el margen)
- La Línea promedio (aquí la línea a mitad de camino entre las dos líneas rojas) será el límite de decisión
esto es muy agradable y fácil, pero encontrar el mejor margen, el problema de optimización no es trivial (es fácil 2D, cuando solo tenemos dos atributos, pero qué pasa si tenemos n dimensiones con n un número muy grande)
para resolver el problema de optimización, usamos los multiplicadores de Lagrange., Para entender esta técnica puede leer los siguientes dos artículos: dualidad multiplicador Langrange y una explicación Simple de por qué multiplicadores Langrange Wroks.
hasta ahora teníamos datos linealmente separables, por lo que podíamos usar una línea como límite de clase. ¿Pero qué pasa si tenemos que lidiar con conjuntos de datos no lineales?,
SVM No Lineales los Conjuntos de Datos
Un ejemplo de no-lineal de los datos es:

En este caso no podemos encontrar una línea recta para separar las manzanas de los limones. Entonces, ¿cómo podemos resolver este problema. ¡Usaremos el truco del Kernel!
la idea básica es que cuando un conjunto de datos es inseparable en las dimensiones actuales, agregue otra dimensión, tal vez de esa manera los datos serán separables., Solo piénsalo, el ejemplo anterior está en 2D y es inseparable, pero tal vez en 3D hay un espacio entre las manzanas y los limones, tal vez hay una diferencia de nivel, por lo que los limones están en el nivel uno y los limones están en el nivel dos. En este caso podemos dibujar fácilmente un hiperplano de separación (en 3D un hiperplano es un plano) entre el nivel 1 y el 2.
Mapping to Higher Dimensions
para resolver este problema no debemos simplemente agregar otra dimensión ciegamente, debemos transformar el espacio para generar esta diferencia de nivel intencionalmente.,
mapeo de 2D a 3D
supongamos que agregamos otra dimensión llamada X3. Otra transformación importante es que en la nueva dimensión los puntos se organizan usando esta fórmula x12 + x22.
Si dibujamos el plano definido por la x2 + y2 fórmula, obtendremos algo como esto:

Ahora tenemos a un mapa de las manzanas y limones (que son sólo simples puntos) a este nuevo espacio. Piénsalo bien, ¿qué hicimos?, Acabamos de utilizar una transformación en la que añadimos niveles basados en la distancia. Si estás en el origen, entonces los puntos estarán en el nivel más bajo. A medida que nos alejamos del origen, significa que estamos subiendo la colina (moviéndonos desde el centro del plano hacia los márgenes) por lo que el nivel de los puntos será más alto., Ahora bien, si tenemos en cuenta que el origen es el limón desde el centro, tendremos algo como esto:
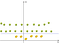
Ahora podemos separar las dos clases. Estas transformaciones se llaman núcleos. Los núcleos más populares son: núcleo polinómico, núcleo gaussiano, función de Base Radial (RBF), núcleo Laplace RBF, núcleo Sigmoid, núcleo Anove RBF, etc. (consulte Funciones del núcleo o una descripción más detallada de los núcleos de aprendizaje automático).,
Asignación de 1D 2D
Otro, ejemplo más sencillo en 2D sería:

Después de usar el kernel y después de todas las transformaciones que vamos a conseguir:

Así que después de la transformación, fácilmente podemos delimitar las dos clases utilizando una única línea.,
en aplicaciones de la vida real no tendremos una simple línea recta, pero tendremos muchas curvas y dimensiones altas. En algunos casos no tendremos dos hiperplanos que separen los datos sin puntos entre ellos, por lo que necesitamos algunas compensaciones, tolerancia para valores atípicos. Afortunadamente, el algoritmo SVM tiene un parámetro llamado regularización para configurar el trade-off y tolerar valores atípicos.
parámetros de ajuste
Como vimos en la sección anterior elegir el núcleo correcto es crucial, porque si la transformación es incorrecta, entonces el modelo puede tener resultados muy pobres., Como regla general, siempre verifique si tiene datos lineales y, en ese caso, siempre use SVM lineal (núcleo lineal). El SVM lineal es un modelo paramétrico, pero un SVM del núcleo RBF no lo es, por lo que la complejidad de este último crece con el tamaño del conjunto de entrenamiento. No solo es más caro entrenar un SVM del núcleo RBF, sino que también tiene que mantener la matriz del núcleo alrededor, y la proyección en este espacio dimensional superior «infinito» donde los datos se vuelven linealmente separables también es más caro durante la predicción., Además, tiene más hiperparámetros para afinar, por lo que la selección del modelo también es más cara. Y por último, ¡es mucho más fácil sobreequipar un modelo complejo!
regularización
El parámetro de regularización (en python se llama C) le dice a la optimización SVM cuánto desea evitar perder la clasificación de cada ejemplo de entrenamiento.
si la C es mayor, la optimización elegirá un hiperplano de margen más pequeño, por lo que la tasa de clasificación de pérdida de datos de entrenamiento será menor.,
por otro lado, si la C es baja, entonces el margen será grande, incluso si habrá ejemplos de datos de entrenamiento miss clasificados. Esto se muestra en los dos gráficos siguientes:

Como se puede ver en la imagen, cuando C es bajo, el margen es mayor (así, implícitamente, que no tiene tantas curvas, la línea no sigue estrictamente los puntos de datos), incluso si dos manzanas que fueron clasificados como de los limones., Cuando la C es alta, el límite está lleno de curvas y todos los datos de entrenamiento se clasificaron correctamente. No se olvide, incluso si todos los datos de entrenamiento se clasificaron correctamente, esto no significa que el aumento de la C siempre aumentará la precisión (debido al sobreajuste).
Gamma
El siguiente parámetro importante es el Gamma. El parámetro gamma define hasta dónde llega la influencia de un solo ejemplo de entrenamiento. Esto significa que Gamma alta considerará solo puntos cercanos al hiperplano plausible y Gamma baja considerará puntos a mayor distancia.,

div 397da36da4″ >
como puede ver, la disminución de la gamma dará como resultado que encontrar el hiperplano correcto considerará puntos a mayores distancias, por lo que se utilizarán más y más puntos (las líneas verdes indican qué puntos se consideraron al encontrar el hiperplano óptimo).
Margin
El último parámetro es el margen. Ya hemos hablado de margen, mayor margen resulta mejor modelo, así que mejor clasificación (o predicción)., El margen debe maximizarse siempre.
ejemplo de SVM usando Python
en este ejemplo usaremos Social_Networks_Ads.archivo csv, el mismo archivo que usamos en el artículo anterior, Ver ejemplo de KNN usando Python.
en este ejemplo escribiré solo las diferencias entre SVM y KNN, ¡porque no quiero repetirme en cada artículo! Si desea la explicación completa sobre cómo podemos leer el conjunto de datos, cómo analizamos y dividimos nuestros datos o cómo podemos evaluar o trazar los límites de decisión, ¡lea el ejemplo de código del capítulo anterior (KNN)!,
debido a que la biblioteca sklearn es una biblioteca Python muy bien escrita y útil, no tenemos demasiado código para cambiar. La única diferencia es que tenemos que importar la clase SVC (SVC = SVM en sklearn) desde sklearn.svm en lugar de la clase KNeighborsClassifier de sklearn.vecino.
después de importar el SVC, podemos crear nuestro nuevo modelo utilizando el constructor predefinido. Este constructor tiene muchos parámetros, pero describiré solo los más importantes, la mayoría de las veces no usarás otros parámetros.,
los parámetros más importantes son:
- kernel: el tipo de kernel a utilizar. Los núcleos más comunes son rbf (este es el valor predeterminado), poly o sigmoid, pero también puede crear su propio núcleo.,
- C: Este es el parámetro de regularización descrito en la sección de parámetros de sintonización
- gamma: esto también fue descrito en la sección de parámetros de sintonización
- Grado: se utiliza solo si el núcleo elegido es poly y establece el grado de polinom
- probabilidad: este es un parámetro booleano y si es true, entonces el modelo devolverá para cada predicción, el vector de probabilidades de pertenecer a cada clase de la variable de respuesta. Así que básicamente te dará las confidencias para cada predicción.,
- encogimiento: esto muestra si desea o no utilizar una heurística de encogimiento en su optimización del SVM, que se utiliza en la optimización mínima secuencial. Su valor predeterminado es true, y si no tiene una buena razón, no cambie este valor a false, porque la reducción mejorará en gran medida su rendimiento, por muy poca pérdida en términos de precisión en la mayoría de los casos.
ahora veamos el resultado de ejecutar este código., El límite de decisión para el conjunto de entrenamiento se ve así:

como podemos ver y como hemos aprendido en la sección de parámetros de sintonización, debido a que la C tiene un valor pequeño (0.1), el límite de decisión es suave.
ahora si aumentamos la C de 0.,De 1 a 100 que vamos a tener más curvas en la decisión de la frontera:

¿Qué pasaría si usamos C=0.1 pero ahora que el aumento de la Gamma de 0,1 a 10? ¡Veamos!

¿Qué pasó aquí? ¿Por qué tenemos un modelo tan malo?, Como has visto en la sección de parámetros de sintonización, high gamma significa que al calcular el hiperplano plausible solo consideramos los puntos que están cerca. Ahora, debido a que la densidad de los puntos verdes es alta solo en la región verde seleccionada, en esa región los puntos están lo suficientemente cerca del hiperplano plausible, por lo que esos hiperplanos fueron elegidos. Tenga cuidado con el parámetro gamma, porque esto puede tener una influencia muy mala sobre los resultados de su modelo si lo establece en un valor muy alto (lo que es un «valor muy alto» depende de la densidad de los puntos de datos).,
para este ejemplo los mejores valores para C y Gamma son 1.0 y 1.0. Ahora si ejecutamos nuestro modelo en el conjunto de pruebas que vamos a conseguir en el siguiente diagrama:

Y la Matriz de Confusión se parece a esto:

Como puede ver, tenemos sólo 3 Falsos Positivos y sólo 4 Falsos Negativos., La precisión de este modelo es del 93%, lo que es un resultado realmente bueno, obtuvimos una mejor puntuación que usando KNN (que tenía una precisión del 80%).
Nota: La precisión no es la única métrica utilizada en ML y tampoco la mejor métrica para evaluar un modelo, debido a la paradoja de precisión. Usamos esta métrica para simplificar, pero más tarde, en el capítulo métricas para evaluar Algoritmos de IA hablaremos sobre la paradoja de precisión y mostraré otras métricas muy populares utilizadas en este campo.,
conclusiones
en este artículo hemos visto un algoritmo de aprendizaje supervisado muy popular y potente, la máquina vectorial de soporte. Hemos aprendido la idea básica, qué es un hiperplano, qué son vectores de soporte y por qué son tan importantes. También hemos visto muchas representaciones visuales, lo que nos ayudó a entender mejor todos los conceptos.
otro tema importante que tocamos es el truco del Kernel, que nos ayudó a resolver problemas no lineales.
Para tener un mejor modelo, vimos técnicas para afinar el algoritmo., Al final del artículo teníamos un ejemplo de código en Python, que nos mostró cómo podemos usar el algoritmo KNN.
como pensamientos finales, me gustaría dar algunos pros & contras y algunos casos de uso populares.,
Pros
- SVN puede ser muy eficiente, ya que utiliza solo un subconjunto de los datos de entrenamiento, solo los vectores de soporte
- funciona muy bien en conjuntos de datos más pequeños, en conjuntos de datos no lineales y espacios de alta dimensión
- Es muy eficaz en los casos en que el número de dimensiones es mayor que el número de muestras
- Puede tener una alta precisión, a veces puede funcionar incluso mejor que las redes neuronales
- /li>
cons
- El tiempo de entrenamiento es alto cuando tenemos grandes conjuntos de datos
- Cuando el conjunto de datos tiene más ruido (i.,E. Las Clases de destino se superponen) SVM no funciona bien
casos de uso populares
- Clasificación de texto
- detección de spam
- Análisis de sentimientos
- reconocimiento basado en aspectos
- reconocimiento basado en aspectos
- reconocimiento de dígitos
