Geometrinen jonot ja Summat | Mark's Trackside

Sarja

sarja on joukko asioita (yleensä numeroita), jotka ovat järjestyksessä.

Geometrinen Sekvenssit

Vuonna Geometrinen sarja jokainen termi on löytynyt kertomalla edellinen termi vakiolla.

yleensä kirjoitamme geometrisen sekvenssin näin:

a, ar, ar2, ar3, …, }

missä:

a on ensimmäinen termi, ja
r on tekijä ehtojen välillä (nimeltään ”yhteistä ratio”)

Mutta ole varovainen, r ei saa olla 0:

Kun t=0, saadaan jono {a,0,0,…} joka ei ole geometrinen

Sääntö

Voimme myös laskea tahansa aikavälillä käyttää Sääntö:

xn = ar(n-1)

(käytämme ”n-1”, koska ar0 on 1 termi)

A Geometrinen sarja voi myös olla pienempiä arvoja:

Esimerkki:

4, 2, 1, 0.5, 0.25, …,

tällä jaksolla on kunkin luvun välillä kerroin 0,5 (puolikas).

Sen Sääntö on xn = 4 × (0.5)n-1

Miksi ”Geometrinen” Järjestyksessä?,

Koska se on kuin lisäämällä mitat geometria:

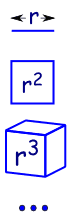	rivi on 1-ulotteinen ja pituus on r
	2 mitat neliön pinta-ala on r2
	3 mitat kuution tilavuus on r3
	jne (kyllä, meillä voi olla 4 ja enemmän ulottuvuuksia matematiikka).,

Geometrinen Sekvenssit ovat joskus kutsutaan Geometrinen Progressions (G. P. n)

Yhteenvetona Geometrinen Sarja

yhteenvetona nämä:

a + ar + ar2 + … + ar(n-1)

(Jokainen termi on arkki, jossa k alkaa 0: sta ja menee jopa n-1)

Me voidaan käyttää tätä kätevä kaava:

on ensimmäinen aikavälillä
r on ”yhteinen suhde” välillä ehdot
n on termien lukumäärä

Mikä on tuo hauska Σ symboli?, Se on nimeltään Sigma-Notaatiota

(kutsutaan Sigma) tarkoittaa ”tiivistää”

– Ja alapuolella ja sen yläpuolella ovat osoittaneet, alkaa ja päättyy arvot:

Se sanoo ”Yhteenvetona n, jossa n menee 1-4. Vastaus=10

kaavaa on helppo käyttää …, vain ”plug in” arvot, r-ja n –

Kaavan

katsotaanpa kaava toiminta:

Esimerkki: Riisinjyvät shakkilaudalla

sivulla Binary Numeroa annamme esimerkin riisinjyvät shakkilaudalla. Kysymys on kysyi:

Kun paikka riisi shakkilauta:

1 viljaa ensimmäinen neliö,
2 jyvät toinen neliö,
4 jyvät kolmannen ja niin edelleen,
…

… kaksinkertaistaa riisinjyvät jokaisella neliöllä …

…, kuinka monta riisinjyvää yhteensä?

Joten meillä on:

a = 1 (ensimmäinen termi)
r = 2 (kaksinkertaistuu joka kerta)
n = 64 (64 ruudut shakkilaudalla)

Niin:

Tulee:

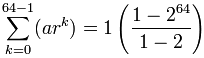
= 1-264-1 = 264 − 1

= 18,446,744,073,709,551,615

Joka on täsmälleen tuloksena saimme Binary Numeroa sivu (luojan kiitos!)

Ja toinen esimerkki, tällä kertaa r-vähemmän kuin 1:

Miksi Kaava Toimii?,

katsotaan, miksi kaava toimii, koska saamme käyttää mielenkiintoista ”temppua”, joka kannattaa tietää.

ensin, kutsu koko summa ”S”: S = A + ar + ar2 + … + ar(n−2)+ ar(n−1)

Seuraava -, kerto-S: n r:S·r = ar + ar2 + ar3 + … + ar(n−1) + arn

huomaa, että S ja S·r ovat samanlaisia?

nyt vähennä ne!

Wow! Kaikki ehdot keskellä siististi peruuttaa.,
(Joka on siisti temppu)

vähentämällä S·t S me saada yksinkertainen tulos:

S − S·r = a − arn

katsotaanpa järjestää sitä löytää S:

Tekijä S: n ja a:S(1−r) = a(1−rn)

Jaa (1−r):S = a(1−rn)(1−r)

Mikä on meidän kaava (ta-da!):

Ääretön Geometrinen Sarja

mitä tapahtuu, kun n menee äärettömään?,

Me voidaan käyttää tätä kaavaa:

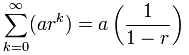
Mutta ole varovainen:

r, on välillä (mutta ei mukaan lukien) -1 ja 1.

ja r ei saa olla 0, koska jono {a,0,0,…} ei ole geometrinen

Joten meidän infnite geometrinen sarja on äärellinen summa, kun suhde on pienempi kuin 1 (ja suurempi kuin -1)

oletetaan, tuoda takaisin meidän edellinen esimerkki, ja katso mitä tapahtuu:

Älä usko minua? Just look at this square:

by conting up 12 + 14 + 18 + …

we end up with the whole thing!,

Toistuva Desimaalin

toisella sivulla kysyimme ”Ei 0.999… yhtä kuin 1?”, no, katsotaan, jos voimme laskea sen: