Nopea Vastaus:
oikea-kulma kolmion:

sini toiminto synti vie kulma θ ja antaa suhde vastapäätä hypotenuusa.
käänteinen sini-toimintoa sin-1 vie suhde oppositehypotenuse ja antaa kulman θ
Ja kosini ja tangentti seuraa samanlainen idea.,
Ja nyt tiedot:
Sini, Kosini ja Tangentti ovat kaikki perustuu Suorakulmaisen Kolmion.
– He ovat hyvin samanlaisia toimintoja … joten katsomme Sinin toimintaa ja sitten kääntäen Sinin oppiaksemme, mistä on kyse.,
Sini Toiminto
Sini kulma θ on:
- pituus puolella Vastapäätä kulma θ
- jaettuna Hypotenuusan pituus
Tai yksinkertaisemmin:
sin(θ) = Vastapäätä / Hypotenuusa.
Sini-Toiminto voi auttaa meitä ratkaisemaan asioita, kuten tämä:
Käänteinen Sini Toiminto
Mutta joskus se on kulma, joka meidän täytyy löytää.
tässä tulee” Käänteissiini”.
se vastaa kysymykseen ”mikä kulma on sini yhtä suuri kuin päinvastainen / hypotenuse?,”
käänteisen sinin symboli on sin-1, tai joskus arcsin.
ne ovat kuin eteen ja taaksepäin!

- synti vie kulmassa ja antaa meille suhde ”vastapäätä/hypotenuusa”
- sin-1 vie suhde ”vastapäätä/hypotenuusa” ja antaa meille kulman.
Esimerkki:
Laskin
 |
laskin painat jotakin seuraavista (riippuen merkki laskin):joko ’2ndF synti” tai ”shift synti’. |
teidän laskin, kokeile syntiä ja sitten sin-1 nähdä, mitä tapahtuu,
Enemmän Kuin Yksi Kulma!
Inverse Sine näyttää vain yhden kulman … mutta on enemmän näkökulmia, jotka voisivat toimia.
esimerkki: tässä on kaksi kulmaa, joissa vastakkainen / hypotenuse = 0.,5
Itse asiassa on olemassa äärettömän monta näkökulmista, koska voit pitää lisäämällä (tai vähentämällä) 360°:
Muista tämä, koska on aikoja, kun todella tarvitset yksi muista näkökulmista!
Tiivistelmä
Sini kulma θ on:
sin(θ) = Vastapäätä / Hypotenuusa.
Käänteinen Sini on :
sin-1 (Vastapäätä / Hypotenuusa) = θ
Mitä Noin ”cos” ja ”tan” … ?
täsmälleen sama ajatus, mutta eri sivusuhteet.,
Kosini
Kosini kulma θ on:
cos(θ) = Vieressä / Hypotenuusa.
Ja Käänteinen Kosini on :
cos-1 (Viereisten / Hypotenuusa) = θ
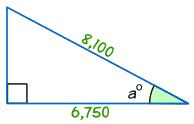
Esimerkki: Etsi koko kulma°
koska a° = Vierekkäisen / Hypotenuusa.
koska a° = 6,750/8,100 = 0.8333…
a° = cos-1 (0, 8333…) = 33.,6° (1 desimaalin tarkkuudella)
Tangentti
Tangentti kulma θ on:
tan(θ) = Vastapäätä / Vieressä
Inverse Tangentti on :
tan-1 (Vastapäätä / Vieressä) = θ
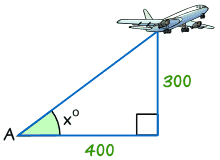
Esimerkki: Löytää koko kulma x°
tan x° = Vastapäätä / Vieressä
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (oikea 1 desimaaliin)
Muuta Nimeä
Joskus sin-1 kutsutaan asin tai arcsin
Myös cos-1 kutsutaan acos tai arccos
Ja tan-1 kutsutaan atan tai arctan
Esimerkkejä:
- arcsin(y) on sama kuin sin-1(y)
- atan(θ) on sama kuin tan-1(θ)
- jne.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- But the Inverse Sine and Inverse Cosine don ’ t ”go on forever” like Sine and Cosine do …
let us look at the example of Cosine.
Tässä on, Kosini ja Käänteisen Kosinin piirretty samaan kuvaajaan:
Kosini ja Käänteinen Kosini
– He ovat peili kuvia (noin lävistäjä)
Mutta miksi Käänteinen Kosini saada hienonnettu pois ylhäältä ja alhaalta (pisteet eivät ole todella osa toiminto) … ?
koska funktiona se voi antaa vain yhden vastauksen
, kun kysymme ” mikä on cos-1 (x) ?,”
Yksi Vastaus, tai Äärettömän Monta Vastausta
Mutta me näimme aiemmin, että on olemassa äärettömän monta vastausta, ja katkoviiva kuvaaja osoittaa tämän.
joten Kyllä vastauksia on äärettömän paljon …
… mutta kuvittele, että kirjoitat 0.5 laskimeen, paina cos-1 ja se antaa sinulle loppumattoman listan mahdollisista vastauksista …
joten meillä on tämä sääntö, että funktio voi antaa vain yhden vastauksen.
Joten, leikkaamalla se pois, kuten että voimme saada vain yksi vastaus, mutta meidän pitäisi muistaa, että siellä voisi olla muiden vastauksia.,
Tangentti ja Inverse Tangentti
Ja tässä on tangentti toiminto ja käänteisen tangentin. Voit nähdä, miten ne ovat peilikuvia (noin lävistäjä) …?

Tangentti

Inverse Tangentti



