helpoin tapa kaapata ajatus kasvava väestö on yksi tut organismi, kuten bakteerin tai cilliate. Kuvassa 1 on Parameciumin populaatio pienessä laboratorion masennusliukumassa. Tässä populaatiossa yksilöt jakautuvat kerran päivässä. Joten, alkaen yksittäinen päivä 0, odotamme, peräkkäisinä päivinä, 2, 4, 8, 16, 32, ja 64 yksilöiden väestöstä., Voimme nähdä tässä, että mitään erityistä päivä, henkilöiden määrä väestöstä on vain kahdesti, mikä numero se oli päivä ennen, niin määrä tänään, kutsuvat sitä N(tänään), on yhtä suuri kuin kaksi kertaa niin paljon kuin eilen, kutsuvat sitä N(eilen), jossa voimme kirjoittaa enemmän tiiviisti kuin N(tänään) = 2N(eilen).
joten on järkevää kirjoittaa tämä as, N(t) = 2n(t – 1), jossa t voisi ottaa mitä tahansa arvoa ollenkaan.,
– Nyt emme voi yleistää tätä ajatusta vähän, jos emme huomaa, että päivä kuusi numero on yhtä suuri kuin kaksinkertainen määrä päivä viisi tai N(6) = 2N(5) ja viides päivä numero on yhtä suuri kuin kaksi kertaa numero päivänä neljä tai N(5) = 2N(4), jne.
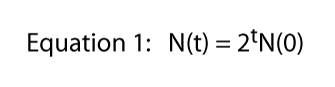
missä t on jokin aikaa ollenkaan (esimerkiksi, jos t = 6, N(6) = 26).
Lopuksi voimme todeta, että tämä yhtälö on johdettu erityinen tilanne on esitetty Kuvassa 1, jossa yksi jako päivässä oli kova ja nopea sääntö., Siinä 2 tulee yhtälöstä 1-jokaisesta yksittäisestä Parameciumista saamme kaksi yksilöä seuraavana päivänä. Tietysti jakoprosentti voi olla mikä tahansa. Jos siellä oli kaksi divisioonaa per päivä, mutta yksi solu aina kuoli, me odottaa kolme henkilöä kustakin yksittäinen ja Yhtälö 1 olisi N(t) = 3tN(0)., Joten jako korko voi olla mikä tahansa numero ja yleinen yhtälö,
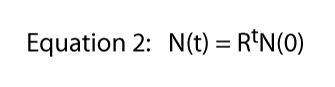
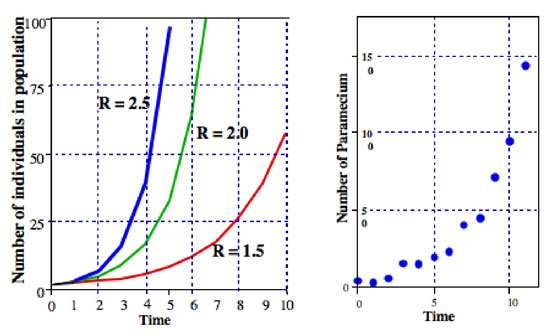
missä R on yleensä kutsutaan rajallinen määrä väestöstä kasvaa (todellinen tapauksessa jakamalla Paramecium rajallinen määrä väestönkasvu on sama jako korko). Kuva 2 havainnollistaa tämän yhtälön eri arvoja R: Se on yleensä kutsutaan eksponentiaalinen yhtälö, ja muodossa tiedot Kuvassa 2 on yleinen muoto nimeltään eksponentiaalinen.,
Jokin arvo R voidaan esittää ääretön määrä tapoja (esimerkiksi, jos R = 16, voimme kirjoittaa R = 8 x 2 tai R = 42, tai R = 32/2, tai R = 2.718282.77). Viimeinen lauseke (R = 2,718282.,77) käyttää tärkeää vakiota, joka voitaisiin palauttaa alkeislaskenta, Eulerin vakio. Ilmaisemalla mitä arvoa R kuin Euler ’ s vakio nostetaan joitakin valtaa on todella erittäin hyödyllistä-se tuo täyden tehon calculus kuvaan.,olize Eulerin vakio e voidaan kirjoittaa Yhtälö 2
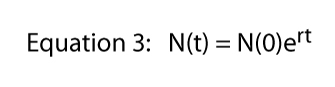
Nyt, jos otamme luonnollinen log molemmin puolin Yhtälö 3 — muista, ln(ex) = x — Yhtälö 3 tulee: ln = ln + rt
Ja jos me alkoi väestön kanssa yksittäinen henkilö (kuten yllä olevassa esimerkissä), meillä on

josta me näemme, että luonnollinen log väestöstä, klo tahansa erityisesti aikaa, on jokin vakio kertaa aika., Vakiosta r käytetään nimitystä luonnollisen lisäyksen luontainen nopeus (kuva 2).
kaikenlaisia mikro-organismien näytteille kuvioita, jotka ovat hyvin lähellä räjähdysmäinen väestönkasvu. Esimerkiksi kuvan 2 oikeassa kädessä on Laboratoriokulttuurissa kasvava Parameciumin populaatio. Kasvukuvio on hyvin lähellä eksponenttiyhtälön kuviota.
Toinen tapa kirjoittaa eksponentiaalinen yhtälö on differentiaaliyhtälö, joka on, joka edustaa kasvun väestöstä sen dynaaminen lomake., Sen sijaan kysyä, mikä on koko väestöstä ajankohtana t, voimme kysyä, mikä on korko, jolla väestö on kasvava hetkellä t. Korko on symboloi kuin dN/dt, joka tarkoittaa yksinkertaisesti ”muutos N suhteellinen muutos vuonna t,” ja jos et muista perus calculus, voimme löytää kasvuvauhti derivoimalla Yhtälö 4, joka antaa meille
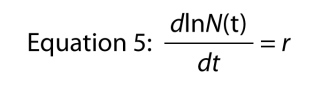
mikä on aika merkittävä, koska se sanoo, että kasvuvauhti kirjaudu numero väestöstä on vakio., Tämä populaation login jatkuva kasvuvauhti on luontainen kasvuvauhti.,
Muista, että muutos loki numero on sama kuin ”per capita” muutos, että numero, mikä tarkoittaa, että voimme kirjoittaa Yhtälön 5

jos me jättää muuttuja t, koska se on selvää, missä se menee, ja sitten me järjestää hieman keksiä
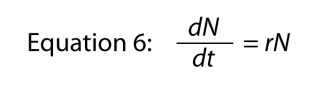
missä parametri r on sisäinen korko luonnollinen kasvu., Perus suhdetta rajallinen kasvu ja sisäinen korko on
r = ln(R)
missä ln viittaa luonnollinen logaritmi. Huomaa, että Yhtälö 6 ja Yhtälö 3 ovat vain erilaisia muotoja sama yhtälö (Yhtälö 3 on integroitu muodossa Yhtälö 6; Yhtälö 6 on eriytetty muodossa Yhtälö 3), ja molemmat voivat olla kutsutaan yksinkertaisesti eksponentiaalinen yhtälö.,

eksponentiaalinen yhtälö on hyödyllinen malli yksinkertainen populaatiot, ainakin suhteellisen lyhyen aikaa., Esimerkiksi, jos laboratorio teknikko tarvitsee tietää, kun bakteeri-kulttuuri saavuttaa tietyn väestön tiheys, eksponentiaalinen yhtälö voidaan antaa ennusteen siitä, milloin populaation koko on saavutettu. Toinen esimerkki on maataloustuholaisten tapauksessa. Kasvinsyöjät ovat aina potentiaalisesti suuria ongelmia kasveille. Kun tällaisten taudinpurkausten kohteena olevat kasvit ovat maatalouskasveja eli viljelykasveja, menetys voi olla hyvin merkittävä sekä viljelijälle että kuluttajalle. Näin ollen tällaisten taudinpurkausten estämiseksi on aina paineita., Toisen maailmansodan jälkeen suurin ase tällaisten tuholaistapausten torjunnassa on ollut kemialliset torjunta-aineet, kuten DDT. Kuitenkin, viime vuosina meillä on tullut ymmärtää, että nämä torjunta-aineet ovat erittäin vaarallisia pitkällä aikavälillä, sekä ympäristölle ja ihmisille. Näin ollen tuholaisten torjumiseksi ruiskutettavien torjunta-aineiden määrää on pyritty rajoittamaan. Tärkein tapa on luoda taloudellinen kynnys, joka on potentiaalisen tuholaisen väestötiheys, jonka alapuolella satovahingot ovat merkityksettömiä (eli ei ole oikeastaan tarpeen suihkuttaa)., Kun tuholaisten väestöstä nousee yli kynnyksen, viljelijän on toteutettava toimia, ja soveltaa jonkinlaista torjunta -, tai muita keinoja valvoa tuholaisia. Kun otetaan huomioon ongelman luonne, on joskus erittäin tärkeää pystyä ennustamaan, milloin tuholainen saavuttaa taloudellisen kynnyksen. Tuholaisten R-arvon tunteminen antaa viljelijälle mahdollisuuden ennustaa, milloin on tarpeen soveltaa jonkinlaista torjuntamenettelyä (kuva 3).
eksponenttiyhtälö on myös hyödyllinen malli intuitiivisten ajatusten kehittämiseksi populaatioista., Klassinen esimerkki on lampi, jossa asuu lilja tyynyjä. Jos jokainen lily pad toistaa itseään (kaksi tyynyt ottaa paikka, jossa yksi pad oli ollut) joka kuukausi, ja se otti, sanovat, kolme vuotta lampi tulla puoli täynnä lilja tyynyt, kuinka paljon kauemmin kestää lampi on täysin peitetty lilja tyynyt? Jos et ajattele liian selvästi, se on houkuttelevaa sanoa, että se vie yhtä paljon aikaa, kolme vuotta, toinen puoli lampi tulla niin täynnä kuin ensimmäinen. Vastaus on tietenkin yksi kuukausi.,
Toinen suosittu esimerkki on kuuluisa muinaisen Egyptin (tai joskus Persian) matemaatikko, joka pyytää maksun kuninkaan muodossa vehnän (joskus riisiä). Yksi jyvä shakkilaudan ensimmäisellä neliöllä, kaksi jyvää toisella neliöllä ja niin edelleen viimeiseen neliöön asti. Faarao ei voi kuvitella, että tällainen yksinkertainen maksu voisi olla paljon, ja niin on samaa mieltä. Hän ei kuitenkaan täysin ymmärtänyt eksponentiaalista kasvua., Koska on 64 ruutua shakkilaudalla, voimme käyttää Yhtälöä 2 määrittää, kuinka monta vehnän on velvollinen maksamaan viimeisen neliö (R nostetaan 64 teho, joka on noin 18,446,744,074,000,000,000 — paljon vehnää todellakin, varmasti enemmän kuin koko valtakunnassa). Nämä esimerkit korostavat usein yllättävää tapaa, jolla eksponentiaalinen prosessi voi johtaa hyvin suuriin joukkoihin hyvin nopeasti.
