
Tässä artikkelissa, opit SVM-tai Support Vector Machine, joka on yksi suosituimmista AI algoritmit (se on yksi top 10 AI algoritmeja) ja noin Kernel Trick, joka käsittelee ei-lineaarisuus ja korkeampia ulottuvuuksia., Me koskettaa aiheista kuten hyperplanes, Lagrangen Kertoimet, meillä on visuaalisia esimerkkejä ja koodi esimerkkejä (samanlainen koodi esimerkissä käytetään KNN-luku) ymmärtämään paremmin tätä erittäin tärkeää algoritmi.
SVM Selitti
Support Vector Machine on valvottu oppiminen algoritmi enimmäkseen käytetään luokittelua, mutta sitä voidaan käyttää myös regressio. Pääajatuksena on, että merkityn datan (koulutustietojen) perusteella algoritmi yrittää löytää optimaalisen hyperplanen, jota voidaan käyttää uusien datapisteiden luokittelussa. Kahdessa ulottuvuudessa hyperplaneetta on yksinkertainen viiva.,
Yleensä oppimisen algoritmi yrittää oppia yleisimpiä ominaisuuksia (mikä erottaa yhden luokan toisesta) luokka ja luokittelu perustuu näiden edustaja ominaisuudet oppinut (siis luokittelu perustuu eroja luokkien välillä). SVM toimii toisin päin. Se löytää samankaltaisimmat esimerkit luokkien välillä. Ne ovat tukivektorit.
esimerkiksi tarkastellaan kahta luokkaa, omenaa ja sitruunaa.,
Muut algoritmit oppivat kaikkein ilmeisintä, kaikkein edustaja ominaisuudet omenat ja sitruunat, kuten omenat ovat vihreitä ja pyöristetty, kun sitruunat ovat keltainen ja soikea muoto.
sen sijaan SVM etsii sitruunoita hyvin muistuttavia omenoita, esimerkiksi keltaisia ja elliptisiä omenoita. Tästä tulee tukivektori. Toinen tukivektori on omenaa muistuttava sitruuna (vihreä ja pyöristetty). Niinpä muut algoritmit oppivat erot samalla, kun SVM oppii yhtäläisyyksiä.,
Jos me visualisoida esimerkiksi edellä 2D, meillä on jotain tällaista:

Kuten me mennä vasemmalta oikealle kaikki esimerkit on luokiteltu omenat kunnes pääsemme keltainen omena. Tästä eteenpäin luottamus siihen, että uusi esimerkki on omena, laskee samalla kun sitruunaluokan luottamus kasvaa., Kun sitruuna luokan luottamus tulee suurempi kuin applen luokan luottamusta, uusia esimerkkejä luokitellaan sitruunat (jossain välissä keltainen omena ja vihreä sitruuna).
näiden tukivektorien perusteella algoritmi yrittää löytää parhaan luokan erottavan hyperplanen. 2D-että hyperplane on line, joten se näyttäisi tältä:

Ok, mutta miksi en piirrä sininen rajan, kuten yllä olevassa kuvassa?, Voisin myös vetää rajoja, kuten tämä:

Kuten näette, meillä on ääretön määrä mahdollisuuksia tehdä päätös rajan. Miten voimme löytää optimaalisen?
Löytää Optimaalinen Hyperplane
Intuitiivisesti paras linja on linja, joka on kaukana sekä omena ja sitruuna esimerkkejä (on suurin marginaali)., On optimaalinen ratkaisu, meillä on maksimoida marginaali molempiin suuntiin (jos meillä on useita luokkia, sitten meidän täytyy maksimoida se ottaen huomioon kunkin luokat).

Joten, jos vertaamme kuva yllä kuva alla, voimme helposti havaita, että ensimmäinen on optimaalinen hyperplane (linja) ja toinen on sub-optimaalinen ratkaisu, koska marginaali on huomattavasti lyhyempi.,

Koska haluamme maksimoida katteet otetaan huomioon kaikki luokat, sen sijaan käyttää yksi marginaali kunkin luokan, käytämme ”global” marginaali, jossa otetaan huomioon kaikki luokat., Tämä marginaali näyttäisi violetti linja seuraavassa kuvassa:

Tämä marginaali on kohtisuorassa rajan ja tasavälinen tukea vektorit.
joten missä meillä on vektorit? Kunkin laskelmat (laskea etäisyys ja optimaalinen hyperplanes) tehdään vektori-avaruus, niin jokainen datapiste pidetään vektori. Avaruuden ulottuvuus määritellään esimerkkien attribuuttien määrällä., Ymmärtää matematiikka takana, Lue tämä lyhyt matemaattinen kuvaus vektorien, hyperplanes ja optimoinnit: SVM ytimekkäästi.
kaiken kaikkiaan tukivektorit ovat datapisteitä, jotka määrittävät hyperplanen sijainnin ja marginaalin. Me kutsumme heitä ”tuki” vektoreita, koska nämä edustavat tiedot pistettä luokkaa, jos menemme yksi heistä, aseman ja/tai marginaali muuttuu. Muiden datapisteiden siirtäminen ei vaikuta hyperplanen marginaaliin tai asemaan.,
tehdä luokituksia, emme tarvitse kaikkea koulutusta tietojen pistettä (kuten tapauksessa KNN), meidän täytyy pelastaa vain tukea vektorit. Pahimmassa tapauksessa kaikki pisteet ovat tukivektoreita, mutta tämä on hyvin harvinaista ja jos se tapahtuu, sinun pitäisi tarkistaa mallisi virheistä tai virheistä.
joten periaatteessa oppiminen vastaa hyperplanen löytämistä parhaalla marginaalilla, joten kyseessä on yksinkertainen optimointiongelma.,/h2>
perus vaiheet SVM ovat:
- valitse kaksi hyperplanes (2D), joka erottaa tietoja ei pisteitä niiden välillä (punaiset viivat)
- maksimoida niiden etäisyys (marginaali)
- keskimääräinen linja (tässä line puolessa välissä kaksi punaista riviä) tulee päätös rajan
Tämä on erittäin mukava ja helppo, mutta löytää paras marginaali, optimointi-ongelma ei ole triviaali (se on helppoa 2D, kun meillä on vain kaksi attribuuttia, mutta mitä jos meillä on N mitat N erittäin suuri määrä)
ratkaista optimointiongelma, käytämme Lagrangen Kertoimet., Ymmärtää tämä tekniikka, voit lukea seuraavat kaksi artikkelia: Kaksinaisuuden Langrange Kertojan ja Yksinkertainen Selitys, Miksi Langrange Kertoimia Wroks.
tähän asti meillä oli lineaarisesti erotettavissa oleva data, joten voisimme käyttää linjaa luokkarajana. Mutta entä jos joudumme käsittelemään epälineaarisia tietokokonaisuuksia?,
SVM Ei-Lineaarinen aineistoja
esimerkki ei-lineaarinen tiedot on:

Tässä tapauksessa emme voi löytää suora viiva erottaa omenoita sitruunat. Miten voimme ratkaista tämän ongelman? Käytämme ytimen temppu!
perusajatus on, että kun tietojoukko on nykyisissä mitoissa erottamaton, lisää toinen ulottuvuus, ehkä näin tieto on erotettavissa., Vain ajatella sitä, esimerkissä on 2D ja se on erottamaton, mutta ehkä 3D on kuilu sen välillä, omenat ja sitruunat, ehkä siellä on tasoero, joten sitruunat ovat tasolla yksi ja sitruunat ovat tasolla kaksi. Tällöin voimme helposti piirtää erottavan hyperplanen (3D a hyperplane on taso) tason 1 ja 2 välillä.
Kartoitus Korkeampi Mitat
tämän ongelman ratkaisemiseksi meidän ei pitäisi vain sokeasti lisätä toisen ulottuvuuden, meidän pitäisi muuttaa niiden tilaa, jotta voimme luoda tämän tason eroa tarkoituksellisesti.,
Mapping from 2D to 3D
oletetaan, että lisäämme toisen ulottuvuuden nimeltä X3. Toinen tärkeä muutos on se, että uudessa ulottuvuudessa pisteet järjestetään tällä formula_12 + x22: lla.
Jos me juoni määrittelemän tason x2 + y2 kaava, saamme jotain tällaista:

Nyt meillä on kartta, omenat ja sitruunat (jotka ovat vain yksinkertainen pistettä) tätä uutta tilaa. Mieti tarkkaan, mitä teimme., Käytimme juuri muutosta, jossa lisäsimme tasoja etäisyyden perusteella. Jos olet alkuperä, niin pisteet ovat alimmalla tasolla. Kun siirrymme pois alkuperää, se tarkoittaa, että olemme kiipeily kukkulan (liikkuvat päässä konetta kohti marginaalit) niin taso pisteet on korkeampi., Nyt jos ajatellaan, että alkuperä on sitruunan keskeltä, meillä on jotain tällaista:
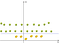
Nyt voimme helposti erottaa kaksi luokkaa. Näitä muunnoksia kutsutaan ytimiksi. Suosittu ytimet ovat: Polynomi-Ytimen, Gaussin Ydin, Radial Basis Function (RBF), Laplace RBF-Ytimen, Sigmoid-Ytimen, Anove RBF-Kernel, jne. (ks Ytimen Toimintoja tai tarkempi kuvaus Koneen Oppimisen Ytimiä).,
Kartoitus 1D 2D
Toinen helpompi esimerkki 2D olisi:

Kun käytät ytimen ja sen jälkeen kaikki muunnokset saamme:

Niin sen jälkeen muutos, voimme helposti rajata kahteen luokkaan käyttäen vain yhdellä rivillä.,
tosielämän sovelluksissa meillä ei ole yksinkertaista suoraa linjaa, mutta kurveja ja mittoja tulee paljon. Joissakin tapauksissa meillä ei ole kahta hyperplanes, joka erottaa tietoja ei pisteitä niiden välillä, joten tarvitsemme joitakin kompromisseja, suvaitsevaisuutta harha. Onneksi SVM-algoritmi on ns laillistaminen parametri määrittää trade-off ja sietää harha.
Tuning-Parametrit
Kuten näimme edellisessä jaksossa oikean ydin on ratkaisevan tärkeää, koska jos muutosta on virheellinen, niin malli voi olla erittäin huonoja tuloksia., Nyrkkisääntönä Tarkista aina, onko sinulla lineaarinen data ja siinä tapauksessa käytä aina lineaarista SVM: ää (lineaarinen ydin). Lineaarinen SVM on parametrinen malli, mutta RBF-kernel SVM ei ole, niin monimutkaisuus jälkimmäinen kasvaa koko koulutus asetettu. Ei vain on kalliimpaa koulutamme RBF-kernel SVM, mutta sinun on myös pidettävä kernel matrix ympäri, ja projektio osaksi tämä ”ääretön” korkea-ulotteinen tila, jossa data muuttuu lineaarisesti separoituvia on kalliimpaa kuin hyvin aikana ennustaminen., Lisäksi sinulla on enemmän hyperparametrejä viritettävänä, joten mallivalikoimakin on kalliimpaa! Ja lopuksi, se on paljon helpompi ylittää monimutkainen malli!
Säännöt
Laillistamiseen Parametri (python se on nimeltään C) kertoo SVM optimointi, kuinka paljon haluat välttää miss luokittelussa kunkin koulutusta esimerkki.
Jos C on korkeampi, optimointi valitsee pienemmän marginaalin hyperplanen, joten harjoitustietojen miss-luokitusaste on pienempi.,
toisaalta, jos C on pieni, niin marginaali on suuri, vaikka siellä on miss luokiteltu koulutus tietojen esimerkkejä. Tämä on esitetty seuraavassa kaksi kaavioita:

Kuten näette kuvan, kun C on alhainen, marginaali on korkeampi (niin epäsuorasti meillä ei ole niin paljon käyriä, linja ei ole tiukasti seuraa tietojen pistettä), vaikka kaksi omenaa olivat luokiteltu sitruunat., Kun C on korkea, raja on täynnä käyriä ja kaikki koulutuksen tiedot oli luokiteltu oikein. Älä unohda, vaikka kaikki koulutuksen tiedot oli luokiteltu oikein, tämä ei tarkoita, että kasvava C aina lisätä tarkkuutta (koska overfitting).
Gamma
seuraava tärkeä parametri on Gamma. Gammaparametri määrittelee, kuinka pitkälle yksittäisen koulutusesimerkin vaikutus ulottuu. Tämä tarkoittaa, että korkea Gamma pitää vain kohtia lähellä uskottavaa hyperplaneetta ja matala Gamma harkitsee pisteitä suuremmalla etäisyydellä.,

Kuten näette, vähentämällä Gamma johtaa, että löytää oikean hyperplane harkitsee pistettä kauempana niin enemmän ja enemmän pisteitä ei saa käyttää (vihreät viivat osoittaa, mitkä kohdat olivat harkita, kun löytää optimaalinen hyperplane).
Marginaali
viimeinen parametri on marginaali. Olemme jo puhuneet marginaali, korkeampi marginaali tulokset parempi malli, joten parempi luokittelu (tai ennustaminen)., Marginaali pitäisi aina maksimoida.
SVM Esimerkiksi käyttämällä Python
tässä esimerkissä käytämme Social_Networks_Ads.csv-tiedosto, sama tiedosto kuin edellisessä artikkelissa, katso KNN esimerkki käyttäen Python.
tässä esimerkissä aion kirjoittaa vain eroja SVM ja KNN, koska en halua toistaa itseäni jokaisessa artikkelissa! Jos haluat koko selitys siitä, miten me voimme lukea tietoja määrittää, kuinka me jäsentää ja jakaa tietoja tai kuinka voimme arvioida tai juoni päätös rajoja, niin lue koodi esimerkki edellisen luvun (KNN)!,
koska sklearnin kirjasto on erittäin hyvin kirjoitettu ja hyödyllinen Python-kirjasto, meillä ei ole liikaa koodia muutettavaksi. Ainoa ero on se, että meidän on tuotava sklearnista SVC-Luokka (SVC = SVM sklearnissa).svm Sklearnin Polvilumpioiden sijasta.naapuri.
Kun olet tuonut SVC, voimme luoda uusi malli käyttää ennalta rakentaja. Tämä rakentaja on monia parametreja, mutta aion kuvata vain tärkeimmät, suurimman osan ajasta et käytä muita parametreja.,
tärkeimmät parametrit ovat:
- ydin: ydin tyyppi, jota käytetään. Yleisin ytimet ovat rbf – (tämä on oletusarvo), poly tai sigmoid, mutta voit myös luoda oman ytimen.,
- C: tämä on laillistaminen parametri on kuvattu Viritys Parametrit kohta
- gamma: tämä oli kuvattu myös viritysparametrien kohta
- tutkinto: sitä käytetään vain, jos valittu ydin on poly ja asettaa aste polinom
- todennäköisyys: tämä on boolen muuttuja, ja jos se on totta, niin malli tulee palauttaa kunkin ennustus, vektori todennäköisyydet kuulua kuhunkin luokkaan vastemuuttuja. Joten pohjimmiltaan se antaa sinulle luottamuksellisuutta jokaisen ennustuksen.,
- kutistuu: tämä osoittaa, onko vai ei haluat kutistuu heuristinen käyttää optimointi SVM, jota käytetään Juokseva Minimaalinen Optimointi. Se on default arvo on true, jos sinulla ei ole hyvää syytä, älä vaihda arvoksi false, koska kutistuu huomattavasti parantaa suorituskykyä, hyvin vähän menetys tarkkuutta useimmissa tapauksissa.
nyt katsotaan lähtö käynnissä tämän koodin., Päätös rajan koulutusta setti näyttää tältä:

Kuten näemme, ja kuten olemme oppineet, Tuning-Parametrit-osiossa koska C on pieni arvo (0.1) päätös raja on sileä.
nyt jos nostamme C: n 0: sta.,1 100 meillä on enemmän käyrät päätös rajan:

Mitä tapahtuu, jos käytämme C=0.1, mutta nyt voimme lisätä Gamma 0,1-10? Katsotaan!

Mitä täällä on tapahtunut? Miksi meillä on niin huono malli?, Kun olet nähnyt Tuning-Parametrit-osiossa, korkea gamma tarkoittaa, että laskettaessa uskottavalta hyperplane pidämme vain pisteitä, jotka ovat lähellä. Nyt, koska tiheys vihreät pisteet on korkea vain valittu vihreä alue, alueen pisteet ovat tarpeeksi lähellä uskottavalta hyperplane, joten ne hyperplanes valittiin. Olla varovainen, gamma-parametri, koska tämä voi olla hyvin huono vaikutus tulokset mallista, jos et aseta se erittäin korkea arvo (mikä on ”hyvin korkea arvo” riippuu tiheys tietoja pistettä).,
tässä esimerkissä C: n ja gamman parhaat arvot ovat 1, 0 ja 1, 0. Nyt, jos me ajaa meidän malli testi asettaa, saamme seuraavan kaavion:

Ja Sekaannusta Matriisi näyttää tältä:

Kuten näette, meillä on vain 3 Vääriä Positiivisia ja vain 4 Vääriä Negatiivisia., Tämän mallin tarkkuus on 93%, mikä on todella hyvä tulos, saimme paremman pistemäärän kuin KNN: llä (jonka tarkkuus oli 80%).
huomaa: tarkkuus ei ole ainoa millilitrassa käytetty metriikka eikä myöskään paras metriikka mallin arvioimiseen Tarkkuusparadoksin vuoksi. Käytämme tätä metriikka yksinkertaisuus, mutta myöhemmin luvussa Metrics arvioida tekoäly algoritmeja puhumme tarkkuus paradoksi ja aion näyttää muita erittäin suosittuja metrics käytetään tällä alalla.,
Johtopäätökset
tässä artikkelissa olemme nähneet erittäin suosittu ja tehokas valvottu oppiminen algoritmi, tukivektorikone. Olemme oppineet perusajatus, mikä on hyperplane, mitä tukea vektorit ja miksi ne ovat niin tärkeitä. Olemme myös nähneet paljon visuaalisia esityksiä, jotka auttoivat meitä ymmärtämään paremmin kaikkia käsitteitä.
toinen tärkeä aihe, johon koskimme, on ytimen temppu, joka auttoi meitä ratkaisemaan epälineaarisia ongelmia.
paremman mallin saamiseksi nähtiin tekniikoita, joilla algoritmi viritettiin., Artikkelin lopussa meillä oli koodiesimerkki Pythonissa, joka näytti meille, miten voimme käyttää KNN-algoritmia.
lopullisina ajatuksina haluaisin antaa joitakin plussia & miinukset ja joitakin suosittuja käyttötapauksia.,
Plussat
- SVN voi olla erittäin tehokas, koska se käyttää vain osan koulutuksen tiedot, vain tukea vektorit
- Toimii hyvin pienempiä aineistoja, ei-lineaarinen aineistoja ja korkea-ulotteinen välilyöntejä
- On erittäin tehokas tapauksissa, joissa määrä mitat on suurempi kuin näytteiden määrä
- Se voi olla korkea tarkkuus, joskus voi suorittaa jopa paremmin kuin neuroverkot
- Ole kovin herkkiä overfitting
Miinukset
- Koulutus on korkea, kun meillä on suurten tietomäärien
- Kun data set on enemmän melua (en.,e. tavoite luokat ovat päällekkäisiä) SVM ei toimi hyvin
Suosittu Käyttää Tapauksissa
- Tekstin Luokittelu
- Havaita spam
- Ilmapiiri analyysi
- Näkökohta perustuva tunnustaminen
- Näkökohta perustuva tunnustaminen
- Käsin numeroinen tunnustaminen
