Tilastot 2 – korrelaatiokerroin ja selitysaste

korrelaatiokerroin

Miten hyvin regressioyhtälö todella edustavat
oman joukko tietoja?
Yksi tapa selvittää vastaus tähän kysymykseen on
tentti korrelaatiokerroin ja selitysaste.,

määrän t, kutsutaan lineaarinen korrelaatiokerroin mittaa voimaa ja
suunta lineaarinen suhde kaksi muuttujaa. Lineaarista korrelaatiota
kerrointa kutsutaan joskus Pearsonin tuotteen momenttikorrelaatiokertoimeksi
kehittäjänsä Karl Pearsonin kunniaksi.
matemaattinen kaava computingr on: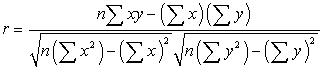

missä n on määrä paria tietojen.,
(Etkö ole iloinen, että sinulla on graafinen laskin, joka laskee tämän kaavan?)
arvo r on sellainen, että -1 < r < +1. + – Merkkejä käytetään positiivisiin
lineaarisiin korrelaatioihin ja negatiivisia lineaarisia korrelaatioita vastaavasti.
Positiivinen korrelaatio: Jos x ja y ovat vahva positiivinen lineaarinen korrelaatio,r on lähellä
+1. R-arvo tasan +1 tarkoittaa täydellistä positiivista istuvuutta., Positiiviset arvot
osoittavat X: n ja y: n muuttujien välisen suhteen siten, että kuten arvot X: lle kasvavat,
y: n arvot myös kasvavat.
Negatiivinen korrelaatio: Jos x ja y on voimakas negatiivinen lineaarinen korrelaatio,r on lähellä
-1. R-arvo tarkalleen -1 osoittaa täydellisen negatiivisen istuvuuden. Negatiiviset arvot
osoittaa suhdetta x ja y siten, että kun arvot x lisätä, arvot
y pienenee.
ei korrelaatiota: jos lineaarista korrelaatiota tai heikkoa lineaarista korrelaatiota ei ole, R on
lähellä 0., Arvo on lähellä nollaa tarkoittaa, että siellä on satunnainen, epälineaarinen suhde
näiden kahden muuttujan välillä
Huomaa, että r on dimensioton suure, eli se ei riipu yksikköä
palveluksessa.
täydellinen korrelaatio ± 1 tapahtuu vain, kun datapisteet kaikki ovat täsmälleen
suoralla. Jos r = +1, Tämän linjan kaltevuus on positiivinen. Jos r = -1, tämän
– linjan kaltevuus on negatiivinen.
korrelaatio on yli 0,8, on yleensä kuvattu niin vahva, kun taas korrelaatio
vähemmän kuin 0.,5 on yleensä kuvattu asweak. Nämä arvot voivat vaihdella tutkittavien tietojen
”tyypin” perusteella. Tieteellistä tietoa hyödyntävä tutkimus voi vaatia vahvempaa
korrelaatiota kuin yhteiskuntatieteellistä dataa hyödyntävä tutkimus.

selitysaste r 2,on hyödyllinen, koska se antaa osuus
varianssi (vaihtelu) yksi muuttuja, joka on ennustettavissa vuodesta toiseen muuttujaan.,
se on toimenpide, jonka avulla voidaan määrittää, miten varma voi olla tehdessään
ennusteita tietystä mallista/graafista.
determinaatiokerroin on suhde selitti vaihtelua koko
vaihtelua.
determinaatiokerroin on sellainen, että 0 < r 2 < 1, ja tarkoittaa voimaa
lineaarinen yhdistyksen välillä x ja y.,
determinaatiokerroin edustaa prosenttia aineistosta, joka on lähimpänä
line of best fit. Esimerkiksi, jos r = 0.922, niin r 2 = 0.850, mikä tarkoittaa, että
85% koko vaihtelu iny voidaan selittää lineaarisesti x
ja y (kuvattu regressio yhtälö). Loput 15% kokonaisvaihtelusta
Y: ssä jää selittämättömäksi.
determinaatiokerroin on mitata, kuinka hyvin regressiolinjan
edustaa tiedot., Jos regressiolinja kulkee täsmälleen jokaisen
scatter-tontin pisteen kautta, se pystyisi selittämään kaiken variaation. Mitä pidemmälle viiva on
pois pisteistä, sitä vähemmän se pystyy selittämään.