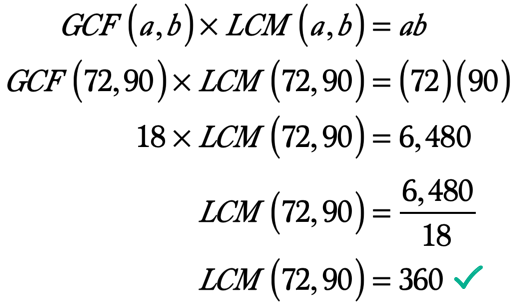lorsque vous étudiiez comment trouver le GCF et le LCM de deux nombres positifs, avez-vous découvert une relation très intéressante entre les deux quantités?

je l’ai fait! Je l’ai découvert par hasard quand j’étais jeune étudiant et je pensais être tombé sur quelque chose de « révolutionnaire”. J’étais tellement excité que je l’ai partagé avec mon professeur., Mais à ma frustration, il m’a regardé dans les yeux et a dit que c’était déjà une déclaration mathématique éprouvée. Je me suis senti découragé pendant un moment, mais je suis retourné à mon travail scolaire et j’ai continué.

Si vous ne l’avez pas encore rencontré, il existe une relation algébrique remarquable entre le plus grand facteur commun (GCF) et le plus petit multiple commun (LCM) de deux nombres. Dans cette leçon, les chiffres que nous voulons sont ceux appartenant à l’ensemble d’entiers positifs seulement.,
ci-dessous est la connexion algébrique entre le GCF et le LCM de deux entiers positifs.
la formule GCF-LCM
avertissement: il n’y a vraiment pas de « Formule GCF-LCM”. Je viens d’inventer le nom pour faciliter la référence. Vous pouvez l’appeler ce que vous voulez tant qu’il sert son but.,
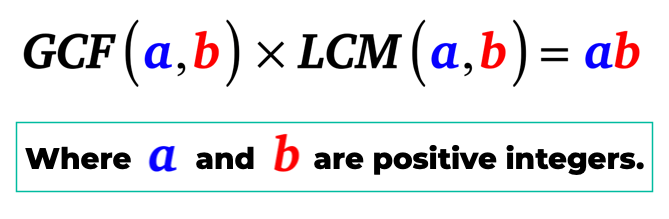
il suffit de mettre, le plus grand facteur commun de a et b, alors que se multiplient pour le plus petit commun multiple de a et b est égale au produit de a et b. Qui est, a et b sont des entiers positifs.
Exemple de Problèmes
Exemple 1: Le PGCD de 12 et 16 est 4. Qu’est-ce que le LCM de 12 et 16?
Vous pouvez déterminer le LCM de 12 et 16 en utilisant l’une des deux méthodes ci-dessous.,
- trouver LCM en utilisant la méthode List
- trouver LCM en utilisant la méthode de factorisation Prime
cependant, il existe un moyen beaucoup plus rapide. Vous pouvez profiter de la « formule GCF-LCM » car vous connaissez les deux entiers et son GCF. Il suffit de brancher les valeurs dans la formule puis de résoudre pour le LCM.
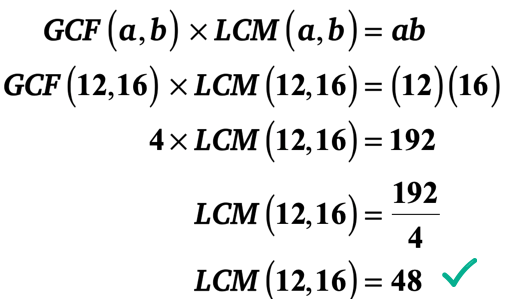
je vous laisse le soin de vérifier que le PPCM de 12 et 16 ans est en effet 48.
exemple 2: Le LCM de 24 et 40 est 120. Qu’est-ce que le FCV de 24 et 40?,
ce problème est exactement le contraire de L’exemple 1 car on vous donne la valeur du LCM au lieu de GCF.
Donc voici les informations que nous connaissons. Nous allons les détailler pour plus de clarté.
▶︎ LCM(24,40) = 120
▶︎ a=24 et b=40 donc ab = \left( {24} \right)\left( {40} \right) = 960
Note Remarque: peu importe les nombres A et B. cela ne changera pas le résultat de la réponse finale. Cependant, c’est une bonne pratique de standardiser votre solution. Je suggère que vous laissiez a être le plus petit entier tandis que b soit le plus grand entier.,
substituons les valeurs connues dans la formule puis résolvons pour le GCF de 24 et 40.
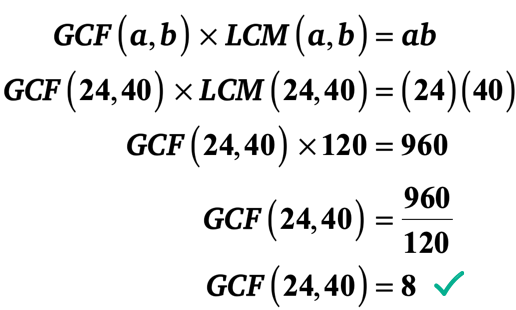
Exemple 3: Trouver le PGCD de 20 et 25, en calculant d’abord le PPCM de 20 et 25.
Ce problème sera un peu différent des exemples #1 et #2. Vous devrez d’abord calculer le Multiple Le moins commun (LCM) de 20 et 25. Après cela, vous pouvez résoudre pour le plus grand facteur commun (GCF) de 20 et 25 en utilisant la formule GCF-LCM.
Donc, nous y voilà!, Afin de trouver le PPCM de 20 et 25, nous allons écrire les premiers multiples de 20 et 25. Le tout premier multiple commun qui apparaît sera notre LCM.
Multiples de 20: 20, 40, 60, 80, 100, 120
Multiples de 25: 25, 50, 75, 100, 125, 150
étant donné que le nombre de 100 se présente comme le premier commun multiple de 20 et 25, alors nous pouvons affirmer que le PPCM de 20 et 25 est de 100.
nous avons maintenant toutes les informations pour utiliser la formule. Voici les valeurs que nous allons substituer dans la formule à résoudre pour le LCM de 20 et 25.,
◉ Le produit de a et de b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ Le PPCM de 20 et 25 → LCM\left( {20,25} \right) = 100
Voici le calcul à résoudre pour le PGCD de 20 et 25:
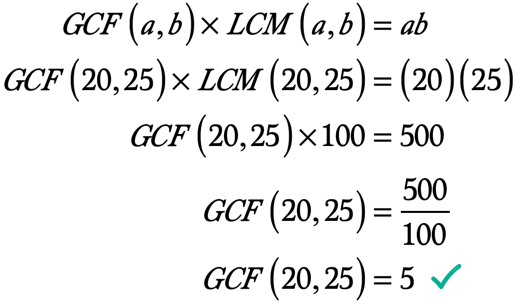
Exemple 4: Trouver le PPCM de 63 et 84 en calculant d’abord le PGCD de 63 et 84.
Ce problème est très similaire à l’exemple #3. La seule différence est que vous calculerez d’abord le GCF au lieu du LCM, comme indiqué par le problème lui-même.,
trouvons tous les facteurs de 63 et 84. Vous pouvez utiliser la technique « rainbow method » pour factoriser les entiers donnés.
notez que le facteur commun le plus important ou le plus élevé entre les deux listes est 21.
Facteurs de 63: 1, 3, 7, 9, 21, 63
Facteurs de 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Donc, le Plus grand Facteur Commun de 63 et 84 21. Ainsi, GCF \ left ({63,84} \right) = 21.,
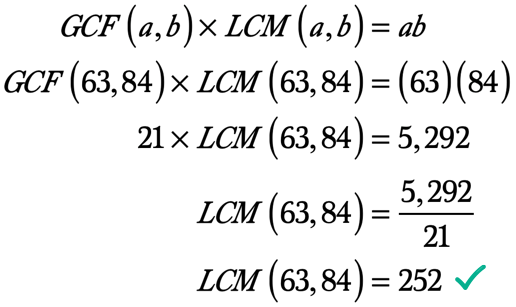
Exemple 5: Trouver le PPCM de 72 et 90 en utilisant le PGCD-PPCM Formule.
Comme nous le savons déjà, nous pouvons trouver le LCM de deux entiers avec la valeur de son GCF en utilisant la formule GCF-LCM.,
Liste des facteurs de 72 et 90, nous avons:
Tous les facteurs de 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Tous les facteurs de 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Lorsque l’on compare les listes de facteurs, nous voyons que le 18 est le facteur commun entre les deux, mais a la plus grande ou de plus grande valeur. Cela signifie que le GCF de 72 et 90 est 18, c’est-à-dire que GCF\left( {72,90} \right) = 18.
Nous sommes maintenant prêts à remplacer les valeurs ci-dessous dans la formule.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Voici le calcul pour trouver le PPCM étant donné que nous connaissons déjà le PGCD de deux entiers et de leurs produits.