Sequenz
Eine Sequenz ist eine Reihe von Dingen (normalerweise Zahlen), die in Ordnung sind.
Geometrische Sequenzen
In einer geometrischen Sequenz wird jeder Term gefunden, indem der vorherige Term mit einer Konstante multipliziert wird.
Im Allgemeinen schreiben wir eine geometrische Sequenz wie folgt:
{a, ar, ar2, ar3, …, }
wobei:
- a der erste Term ist und
- r der Faktor zwischen den Termen ist (das „gemeinsame Verhältnis“genannt)
Aber seien Sie vorsichtig, r sollte nicht 0 sein:
- Wenn r=0 ist,erhalten wir die Sequenz {a,0, 0,…} was nicht geometrisch ist
Die Regel
Wir können auch jeden Begriff mit der Regel berechnen:
xn = ar(n-1)
(Wir verwenden „n-1“, weil ar0 für den 1. Term ist)
Eine geometrische Sequenz kann auch kleinere und kleinere Werte haben:
Beispiel:
> 4, 2, 1, 0.5, 0.25, …,
Diese Sequenz hat einen Faktor von 0,5 (eine Hälfte) zwischen jeder Zahl.
Die Regel ist xn = 4 × (0.5)n-1
Warum „Geometrischen“ – Folge?,
Weil es so ist, als würde man die Abmessungen in der Geometrie erhöhen:
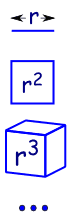 |
Eine Zeile ist eindimensional und hat eine Länge von r |
| in 2 Dimensionen hat ein Quadrat eine Fläche von r2 | |
| in 3 Dimensionen hat ein Würfel Volumen r3 | |
| etc (ja, wir können 4 und mehr Dimensionen in Mathematik haben)., |
Geometrische Sequenzen werden manchmal als geometrische Progressionen (G. P. ‚ s) bezeichnet
Summieren einer geometrischen Reihe
Um diese zu summieren:
a + ar + ar2 + … + ar (n-1)
(Jeder Term ist ark, wobei k bei 0 beginnt und bis zu n-1 geht)
Wir können diese praktische Formel verwenden:

a ist der erste Term
r ist das „gemeinsame Verhältnis“ zwischen Termen
n ist die Anzahl der Terme
Was ist das lustige Σ-Symbol?, Es heißt Sigma Notation
| (genannt Sigma) bedeutet „summieren“ |
Und unten und oben werden die Anfangs-und Endwerte angezeigt:
Es heißt „Sum up n where n goes from 1 to 4. Antwort=10
Die Formel ist einfach zu bedienen …, einfach die Werte von a, r und n
Mit der Formel
“ einstecken“Lassen Sie uns die Formel in Aktion sehen:
Beispiel: Reiskörner auf einem Schachbrett

Auf der Seite Binärziffern geben wir ein Beispiel für Reiskörner auf einem Schachbrett. Die Frage wird gestellt:
Wenn wir Reis auf ein Schachbrett legen:
- 1 Korn auf dem ersten Platz,
- 2 Körner auf dem zweiten Platz,
- 4 Körner auf dem dritten und so weiter,
- …
… verdoppelung der Reiskörner auf jedem Quadrat …
…, wie viele Reiskörner insgesamt?
So haben wir:
- a = 1 (der erste Term)
- r = 2 (verdoppelt sich jedes Mal)
- n = 64 (64 Quadrate auf einem Schachbrett)
So:

Wird:
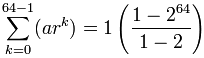
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Das war genau das Ergebnis, das wir auf der Seite mit den Binärziffern erhalten haben (Gott sei Dank!)
Und ein weiteres Beispiel, diesmal mit r weniger als 1:
Warum funktioniert die Formel?,
Mal sehen, warum die Formel funktioniert, weil wir einen interessanten „Trick“ verwenden können, der wissenswert ist.
Beachten Sie, dass S und S·r ähnlich sind?
Subtrahiere sie jetzt!
Wow! Alle Begriffe in der Mitte ordentlich abbrechen.,
(Was ein netter Trick ist)
Durch Subtrahieren von S·r von S erhalten wir ein einfaches Ergebnis:
S − S·r = a − arn
Ordnen wir es neu an, um S zu finden:
Das ist unsere Formel (ta-da!):

Unendliche Geometrische Reihe
was passiert Also, wenn n unendlich?,
Wir können diese Formel verwenden:
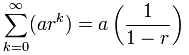
Aber seien Sie vorsichtig:
r muss zwischen -1 und 1
liegen und r sollte nicht 0 sein, da die Sequenz {a, 0, 0,…} ist nicht geometrisch
Unsere infnite geometrische Reihe hat also eine endliche Summe, wenn das Verhältnis kleiner als 1 (und größer als -1)
Bringen wir unser vorheriges Beispiel zurück und sehen, was passiert:
|
Glauben Sie mir nicht? Schauen Sie sich dieses Quadrat an: Durch Addieren 12 + 14 + 18 + … am Ende haben wir das Ganze!, |
 |
Wiederkehrende Dezimalzahl
Auf einer anderen Seite fragten wir “ Does 0.999… gleich 1?“nun, lassen Sie uns sehen, ob wir es berechnen können:



