szekvencia
a szekvencia olyan dolgok halmaza (általában számok), amelyek sorrendben vannak.

Geometriai szekvenciák
Geometriai sorrendben minden kifejezést úgy találunk, hogy az előző kifejezést egy állandóval megszorozzuk.
általában egy ilyen geometriai sorrendet írunk:
{a, ar, ar2, ar3,…, }
ahol:
- a az első kifejezés, és
- r a kifejezések közötti tényező (az úgynevezett “közös Arány”)
de légy óvatos, r nem lehet 0:
- amikor r=0, megkapjuk a {a,0,0 sorrendet…} ami nem geometriai
A Szabály
Mi is számítani bármilyen kifejezés használata a Szabály, hogy:
xn = ar(n-1)
(használjuk az “n-1” mert ar0 az 1. kifejezés)
Egy Mértani Sorozat is kisebb értékek:
Példa:
4, 2, 1, 0.5, 0.25, …,
Ez a szekvencia 0, 5 (fél) tényezővel rendelkezik az egyes számok között.
szabálya xn = 4 × (0,5)n-1
miért “Geometriai” szekvencia?,
Mert ez olyan, mint a növekvő méretek geometria:
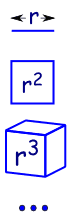 |
egy vonal, 1-dimenziós, majd egy hossza, r |
| 2 méretek négyzet területe r2 | |
| 3 dimenziós kocka van kötet r3 | |
| stb. (igen, mi lehet 4 vagy több méretek matematika)., |
a geometriai szekvenciákat néha Geometriai Progresszióknak (G. P. ‘ S)
Geometriai sorozat összegzése
ezek összegzésére:
a + ar + ar2+… + ar (n-1)
(minden kifejezés ark, ahol k kezdődik 0 és megy fel n-1)
tudjuk használni ezt a praktikus képlet:

a az első kifejezés
r a” közös Arány ” kifejezések között
n a kifejezések száma
mi ez a vicces Σ szimbólum?, Ez az úgynevezett Sigma Jelölés
| (az úgynevezett Sigma) azt jelenti, hogy “összefoglalva” |
alatt, illetve felette látható a kezdő, illetve befejező értékek:
Azt mondja “összefoglalva n, ahol n megy 1-től 4. Válasz=10
a képlet könnyen használható …, csak “csatlakoztassa” az értékeket a, r és n
képlet segítségével
lássuk a képletet akcióban:
példa: rizsszemek egy sakktáblán

az oldalon bináris számjegyek adunk egy példát a szemek a rizs egy sakktábla. A kérdés a következő:
amikor rizst helyezünk egy sakktáblára:
- 1 gabona az első téren,
- 2 szem a második téren,
- 4 szem a harmadik, és így tovább,
- …
… megduplázva a rizsszemeket minden téren …
…, hány szem rizs összesen?
Tehát:
- a = 1 (az első kifejezés)
- r = 2 (páros minden alkalommal)
- n = 64 (64 négyzet egy sakktábla)
Tehát: 
Válik:
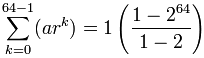
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Ami pontosan az volt az eredménye van a Bináris Számjegy oldal (hála az égnek!)
és egy másik példa, ezúttal r kevesebb, mint 1:
miért működik a képlet?,
lássuk, miért működik a képlet, mert egy érdekes “trükköt” használunk, amelyet érdemes tudni.
figyeljük meg, hogy s és S·r hasonlóak?
most vonjuk le őket!
Wow! A közepén lévő összes kifejezés szépen megszűnik.,
(ami egy ügyes trükk)
az S·r kivonásával egyszerű eredményt kapunk:
S − s·r = a − arn
átrendezzük, hogy S:
melyik a képletünk (ta-da!):

végtelen Geometriai sorozat
Tehát mi történik, ha n A végtelenbe megy?,
ezt a képletet használhatjuk:
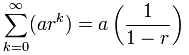
de légy óvatos:
r között kell lennie (de nem tartalmazza) -1 és 1
és r nem lehet 0,mert a szekvencia {a,0, 0,…} nem geometriai
tehát infnite geometriai sorozatunk véges összeggel rendelkezik, ha az arány kisebb, mint 1 (és nagyobb, mint -1)
hozzuk vissza korábbi példánkat, és nézzük meg, mi történik:
|
ne higgy nekem? Csak nézd meg ezt a négyzetet: összeadásával 12 + 14 + 18 + … mi a végén az egészet!, |
 |
ismétlődő decimális
egy másik oldalon megkérdeztük: “nem 0.999… egyenlő 1?”nos, nézzük meg, hogy ki tudjuk-e számítani:


