a növekvő populáció elképzelésének legegyszerűbb módja egyetlen sejtes organizmus, például baktérium vagy cilliate. Az 1. ábrán a Paramecium populációját egy kis laboratóriumi depressziós csúszdában ábrázolják. Ebben a populációban az egyének naponta egyszer osztódnak. Így, kezdve egyetlen egyén napján 0, elvárjuk, egymást követő napokban, 2, 4, 8, 16, 32, és 64 fő a lakosság körében., Itt láthatjuk, hogy bármely adott napon a népességben az egyének száma egyszerűen kétszer annyi, mint az előző nap, tehát a mai szám, n (ma), egyenlő a tegnapi szám kétszeresével, hívja N(tegnap), amelyet kompaktabban írhatunk, mint N(ma) = 2N(tegnap).
tehát érdemes ezt írni, N(t) = 2n(t – 1), ahol t egyáltalán bármilyen értéket felvehet.,
most egy kicsit általánosíthatjuk ezt az elképzelést, ha megjegyezzük, hogy a hatodik napon a szám kétszerese az ötödik napnak, vagy N(6) = 2N(5), az ötödik napon pedig a szám kétszerese a negyedik napnak, vagy N(5) = 2N(4) stb.
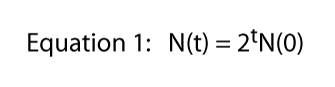
ahol T egyáltalán áll (pl. ha t = 6, N(6) = 26).
végül megjegyezzük, hogy ez az egyenlet az 1. ábrán látható konkrét helyzetből származik, ahol napi egy osztás volt a kemény és gyors szabály., Ez az, ahol a 2 származik egyenlet 1 – minden egyes Paramecium kapunk két személy a következő napon. Természetesen a megosztási arány bármi lehet. Ha naponta két osztás lenne, de egy sejt mindig meghalna, minden egyes egyéntől három egyént várnánk, és az 1.egyenlet N(t) = 3TN(0) lenne., Szóval a divízió arány lehetséges egyáltalán, valamint az általános egyenlet válik,
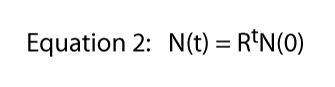
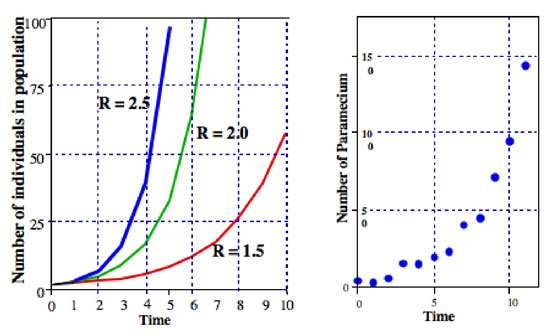
ahol R általában nevezik, a véges arány a népesség növekedése (a tényleges esetben, ha elosztjuk Paramecium a véges arány a népesség növekedése egyenlő a divízió arány). A 2. ábrán ezt az egyenletet szemléltetjük az R különböző értékeire. általában exponenciális egyenletnek nevezik, és a 2.ábrán szereplő adatok formája az exponenciális általános forma.,
az R bármely értéke végtelen számú módon ábrázolható(pl. ha R = 16, írhatnánk R = 8 x 2, vagy R = 42, vagy R = 32/2, vagy R = 2.718282.77). Ez az utolsó kifejezés (R = 2.718282.,77) egy fontos állandót használ, amelyet az elemi kalkulusból, Euler állandójából lehet felidézni. Az R bármilyen értékének kifejezése, mint Euler állandója, amelyet valamilyen hatalomra emelnek, valójában rendkívül hasznos — a kalkulus teljes erejét hozza a képbe.,olize Euler konstans, mint e írhatunk Egyenlet 2
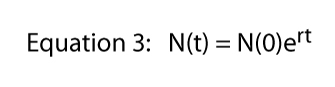
ha a természetes napló mindkét oldalán 3. Egyenlet — emlékszel ln(ex) = x — 3. Egyenlet válik: ln = ln + rt
ha kezdtük, hogy a lakosság egyszeri, egyedi (mint a fenti példában), van

a, amely azt látjuk, hogy a természetes napló a lakosság, adott időben, egy állandó, hányszor idő., Az állandó r-t a természetes növekedés belső sebességének nevezik (2.ábra).
mindenféle mikroorganizmus olyan mintákat mutat, amelyek nagyon közel állnak az exponenciális népesség növekedéséhez. Például a 2.ábra jobb oldali grafikonjában egy laboratóriumi kultúrában növekvő Paramecium populáció. A növekedés mintája nagyon közel áll az exponenciális egyenlet mintájához.
Az exponenciális egyenlet írásának másik módja a differenciálegyenlet, vagyis a populáció dinamikus formájának növekedését képviseli., Ahelyett, hogy azt kérdezi, milyen a méret a lakosság a t időpontban, kérdezzük meg, mi az a kamatláb, amely a népesség növekszik, a t időpontban. Az arány szimbolizálja, mint dN/dt, ami egyszerűen azt jelenti, “a változás a N képest változás t -,” ha emlékszel, az alap matek, meg tudjuk találni, hogy a növekedés üteme által differenciáló Egyenlet 4, ami számunkra
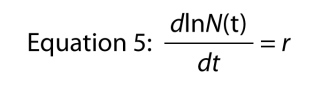
ami elég figyelemre méltó, mert azt mondja, hogy a növekedés üteme a napló száma a népesség állandó., A népesség naplójának állandó növekedési üteme a növekedés belső üteme.,
Emlékezzünk vissza, hogy a változás mértéke a napló számos ugyanaz, mint az “egy főre jutó” változás ez a szám, ami azt jelenti, hogy tudunk írni Egyenlet 5

ahol hagyni a változó t, mivel nyilvánvaló, hogy hova megy, aztán áttoljuk egy kicsit, hogy dolgozzon ki
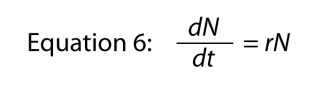
ha a paraméter r, ismét a belső kamatláb a természetes szaporodás., A véges növekedési ráta és az intrinsic rate közötti alapvető kapcsolat
r = ln(R)
, ahol az ln a természetes logaritmusra utal. Vegye figyelembe, hogy a 6. egyenlet és a 3. egyenlet csak ugyanazon egyenlet különböző formái (a 3. egyenlet a 6. egyenlet integrált formája; a 6. egyenlet a 3. egyenlet differenciált formája), és mindkettőt egyszerűen exponenciális egyenletnek lehet nevezni.,

az exponenciális egyenlet az egyszerű populációk hasznos modellje, legalább viszonylag rövid ideig., Például, ha egy laboratóriumi technikusnak tudnia kell, hogy a bakteriális kultúra mikor ér el egy bizonyos népsűrűséget, az exponenciális egyenlet felhasználható arra, hogy előrejelzést adjon arról, hogy pontosan mikor éri el ezt a népességméretet. Egy másik példa a mezőgazdasági kártevők esetében. A növényevők mindig potenciálisan jelentős problémák a növények számára. Amikor az ilyen kitöréseknek kitett növények mezőgazdasági, azaz növények, a veszteség nagyon jelentős lehet mind a mezőgazdasági termelők, mind a fogyasztók számára. Így mindig van nyomás az ilyen kitörések megelőzésére., A második világháború óta az ilyen kártevők kitörése elleni küzdelem legfontosabb fegyvere a kémiai peszticidek, például a DDT. Az elmúlt években azonban rájöttünk, hogy ezek a peszticidek hosszú távon rendkívül veszélyesek mind a környezet, mind az emberek számára. Következésképpen mozgás történt a kártevők elleni küzdelemre permetezett peszticidek mennyiségének korlátozására. Ennek fő módja egy gazdasági küszöb megállapítása, amely a potenciális kártevő népsűrűsége, amely alatt a növény károsodása jelentéktelen (azaz nem igazán szükséges permetezni)., Amikor a kártevőállomány e küszöbérték fölé emelkedik, a gazdálkodónak lépéseket kell tennie, és valamilyen peszticidet vagy más eszközt kell alkalmaznia a kártevő ellenőrzésére. Tekintettel a probléma jellegére, néha rendkívül fontos megjósolni, hogy a kártevő mikor éri el a gazdasági küszöböt. A kártevő fajra vonatkozó R ismerete lehetővé teszi a mezőgazdasági termelő számára, hogy megjósolja, mikor kell valamilyen ellenőrzési eljárást alkalmazni (3.ábra).
Az exponenciális egyenlet hasznos modell a populációkkal kapcsolatos intuitív ötletek kidolgozására is., A klasszikus példa egy tó, amelyben liliompárnák élnek. Ha minden liliomszál reprodukálja magát (két párna a hely, ahol egy pad volt) minden hónapban tartott, mondjuk, három év a tó lenni félig tele liliom párna, meddig fog tartani a tó teljesen borított liliom párna? Ha nem hagyja abba a túl világos gondolkodást, csábító azt mondani, hogy ugyanolyan sok időt, három évet vesz igénybe, amíg a tó második fele annyira megtelik, mint az első. A válasz természetesen egy hónap.,
egy másik népszerű példa a közmondásos ókori egyiptomi (vagy néha perzsa) matematikus, aki a királytól búzaszemek (néha rizs) formájában kér fizetést. Egy szem a sakktábla első négyzetén, két szem a második téren, stb., Az utolsó négyzetig. A fáraó nem tudja elképzelni, hogy egy ilyen egyszerű kifizetés sokat jelenthet,így egyetért. De nem értékelte teljes mértékben az exponenciális növekedést., Mivel a sakktáblán 64 négyzet van, a 2.egyenletet használhatjuk annak meghatározására, hogy hány búzaszemet kell fizetni az utolsó téren (R a 64. hatalomra emelkedik, ami körülbelül 18,446,744,074,000,000,000 — sok búza valóban, minden bizonnyal több, mint az egész királyságban). Ezek a példák hangsúlyozzák azt a gyakran meglepő módszert, amellyel az exponenciális folyamat nagyon nagy számokhoz vezethet nagyon gyorsan.
