Gyors Válasz:
egy derékszögű háromszög:

A szinusz függvény sin veszi szög θ ad az arány, szemben átfogó
Az inverz szinusz függvény sin-1 telik az arány oppositehypotenuse ad szög θ
, Majd a koszinusz, valamint érintő kövesse egy hasonló ötlet.,
és most a részletekért:
szinusz, koszinusz és tangens mind derékszögű háromszög
nagyon hasonló függvények … tehát megnézzük a szinusz funkciót, majd inverz szinuszot, hogy megtudjuk, miről szól.,
Szinusz Függvény
A Szinusz a szög θ:
- a hossza a Szemközti oldalon, szög θ
- osztva a hossza az Átfogó
– Vagy egyszerűen:
sin(θ) = Ellenkezője / Átfogó
A Szinusz Függvény segíthet megoldani a dolgokat, mint ez:
Inverz Szinusz Függvény
De néha az a szög, meg kell találnunk.
itt jön be az” inverz szinusz”.
megválaszolja a kérdést: “milyen szög van szinusz egyenlő az ellenkező/hipotenusszal?,”
az inverz szinusz szimbóluma sin-1, vagy néha arcsin.
olyanok, mint előre-hátra!

- sin szöget vesz fel, és megadja nekünk az”ellenkező/hipotenusz “
- sin-1 arányt, és megadja nekünk a szöget.
példa:
számológép
 |
a számológépen nyomja meg az alábbiak egyikét (a számológép márkájától függően):vagy “2ndf sin” vagy “shift sin”. |
a számológépen próbálja meg használni a sin, majd a sin-1-et, hogy megnézze, mi történik
több mint egy szög!
inverz szinusz csak egy szöget mutat … de vannak olyan szögek, amelyek működhetnek.
példa: itt van két szög, ahol ellentétes / hypotenuse = 0.,5
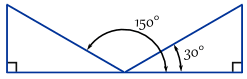
valójában végtelenül sok szög van, mert folyamatosan hozzáadhatja (vagy kivonhatja) 360°:
ne feledje ezt, mert vannak idők, amikor valóban szüksége van egy másik szögre!
összefoglaló
a θ szög szinusza:
sin(θ) = ellentétes / θenuse
és inverz szinusz:
sin-1 (Oppos / hypotenuse) =
mi a helyzet a “cos” és a “tan” … ?
pontosan ugyanaz az ötlet, de különböző oldalarányok.,
Koszinusz
A Koszinusz a szög θ:
cos(θ) = a Szomszédos / Átfogó
Illetve Inverz Koszinusz van :
cos-1 (Szomszédos / Átfogó) = θ
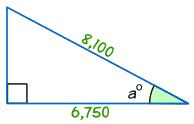
Példa: keresd meg a méret szög°
mert° = Szomszédos / Átfogó
mert° = 6,750/8,100 = 0.8333…
a° = cos-1 (0, 8333…) = 33.,6° (1 tizedesjegy pontossággal)
Érintő
A Tangensét szög θ:
tan(θ) = Ellenkezője / Szomszédos
Tehát Inverz Tangens van :
tan-1 (Szemben / Mellett) = θ
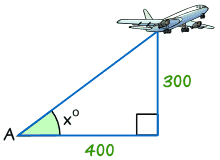
Példa: Keresse meg a méret szög x°
tan x° = Ellenkezője / Szomszédos
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (helyes 1 tizedes)
más nevek
néha sin-1 nevezik asin vagy arcsin
hasonlóképpen cos-1 nevezzük acos vagy arccos
és tan-1 nevezzük atan vagy arctan
példák:
- arcsin(y) ugyanaz, mint a sin-1(y)
- atan(θ/H2>) ugyanaz, mint a tan-1(θ)
- stb.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- de az inverz szinusz és inverz koszinusz nem “folytatódik örökké”, mint a szinusz és a koszinusz …
nézzük meg a koszinusz példáját.
Itt a Koszinusz, illetve Inverz Koszinusz ábrázoljuk az azonos grafikon:
Koszinusz, illetve Inverz Koszinusz
Ezek a tükör a képeket (az átlós)
De miért Inverz Koszinusz kap levágta a felső, illetve alsó (a pontok nem igazán része a funkció) … ?
mert függvénynek lenni csak egy választ adhat
amikor megkérdezzük: “mi a cos-1 (x)?,”
egy válasz vagy végtelenül sok válasz
de korábban láttuk, hogy végtelenül sok válasz van, és a grafikonon a pontozott vonal ezt mutatja.
tehát igen, végtelenül sok válasz van …
… de képzeld el, hogy 0.5-öt írsz be a számológépedbe, nyomd meg a cos-1 gombot, és ez egy soha véget nem érő listát ad a lehetséges válaszokról …
tehát van ez a szabály, hogy egy függvény csak egy választ adhat.
tehát úgy, hogy levágjuk, csak egy választ kapunk, de emlékeznünk kell arra, hogy más válaszok is lehetnek.,
tangens és inverz tangens
és itt van a tangens függvény és inverz tangens. Láthatja, hogy ezek tükörképek (az átlóról) …?

Tangent

inverz Tangent



