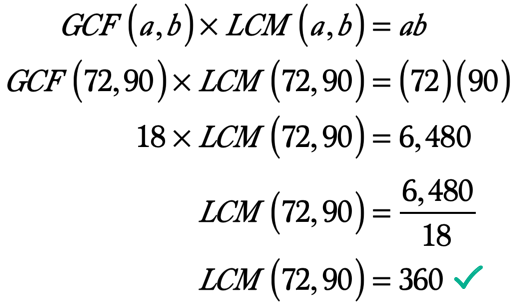amikor két pozitív szám GCF és LCM-jét tanulmányozta, felfedezett egy nagyon érdekes kapcsolatot a két mennyiség között?

i did! Valójában véletlenül fedeztem fel, amikor fiatal diák voltam, és azt hittem, hogy valami “forradalmi”dologba botlottam. Annyira izgatott voltam, hogy megosztottam a tanárommal., Csalódottságomra azonban a szemembe nézett, és azt mondta, hogy ez már bizonyított matematikai kijelentés. Egy pillanatra elkedvetlenedtem, de visszamentem az iskolai munkámba, és nyomtam tovább.

Ha még nem találkozott vele, figyelemre méltó algebrai kapcsolat vagy kapcsolat áll fenn a két szám legnagyobb közös tényezője (GCF) és a legkisebb közös többszörös (LCM) között. Ebben a leckében a kívánt számok azok, amelyek csak a pozitív egész számok halmazához tartoznak.,
az alábbi két pozitív egész algebrai kapcsolata a GCF és az LCM között.
A GCF-LCM Formula
figyelmeztetés: valójában nincs olyan dolog, mint a”GCF-LCM Formula”. Csak kitaláltam a nevet, hogy könnyebb legyen. Lehet nevezni, amit akarsz, amíg ez szolgálja a célját.,
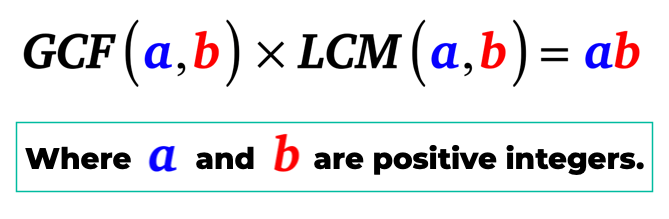
/div > egyszerűen fogalmazva, az A és B legnagyobb közös tényezője, ha az A és B legkisebb közös többszörösére szorozzuk, egyenlő az A és B szorzatával, azaz az A és B pozitív egészek.
Példaproblémák
1.példa: a 12-es és 16-os GCF 4. Mi a 12-es és 16-os LCM?
az alábbi két módszer bármelyikével meghatározható a 12-es és 16-os LCM.,
- LCM megtalálása a
- LCM megtalálása a
elsődleges faktorizációs módszerrel azonban sokkal gyorsabb módszer létezik. Kihasználhatja a” GCF-LCM Formula ” előnyeit, mivel ismeri a két egész számot és annak GCF-jét. Csak csatlakoztassa az értékeket a képletbe, majd oldja meg az LCM-et.
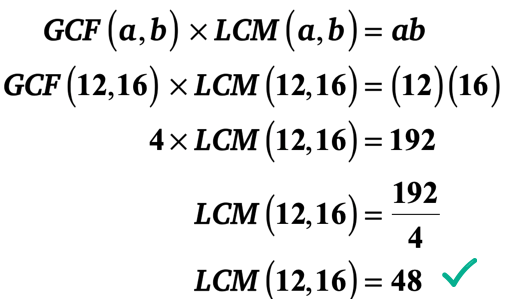
hagyom, hogy ellenőrizze, hogy a 12-es és 16-os LCM valóban 48-e.
2.példa: a 24-es és 40-es LCM 120. Mi a 24-es és 40-es GCF?,
Ez a probléma pontosan ellentétes az 1. példával, mert a GCF helyett az LCM értékét kapja.
tehát ezek az általunk ismert információk. Tételezzük fel őket az egyértelműség érdekében.
▶︎ LCM (24,40) = 120
▶︎ a=24 és b=40 ezért ab = \bal ({24} \jobb)\bal ({40} \jobb) = 960
📌 megjegyzés: nem igazán számít, hogy mely számok a és b. nem változtatja meg a végső válasz kimenetelét. Azonban ez egy jó gyakorlat, hogy szabványosítsa a megoldást. Azt javaslom, hogy hagyja, hogy egy legyen a kisebb egész, míg b a nagyobb egész szám.,
helyettesítsük az ismert értékeket a képletbe, majd oldjuk meg a 24-es és 40-es GCF-et.
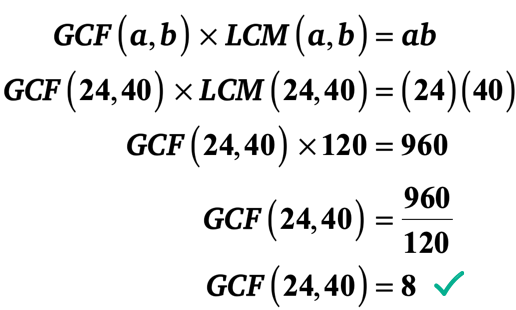
3.példa: keresse meg a 20-as és 25-ös GCF-et a 20-es és 25-ös LCM első kiszámításával.
Ez a probléma kissé eltér az 1. és 2. példától. Először a 20 és 25 legkisebb közös többszörösét (LCM) kell kiszámítania. Ezt követően a GCF-LCM képlet segítségével megoldhatja a 20 és 25 legnagyobb közös tényezőjét (GCF).
tehát itt vagyunk!, A 20-as és 25-ös LCM megtalálásához a 20-as és a 25-ös első párszorosát írjuk meg. Az első közös többszörös, amely megjelenik, az LCM lesz.
Többszöröse 20: 20, 40, 60, 80, 100, 120
Többszöröse 25: 25, 50, 75, 100, 125, 150
Mivel ez a szám 100 mutatja fel, mint az első közös többszörös, 20, 25, akkor kijelenthetjük, hogy a LCM 20 25 100.
most már minden információnk van a képlet használatához. Az alábbiakban azokat az értékeket mutatjuk be, amelyeket a 20-as és 25-ös LCM-re megoldandó képletbe helyettesítünk.,
◉ A termék, illetve b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ A LCM 20 25 → LCM\left( {20,25} \right) = 100
Itt a számítás, hogy megoldja a GCF 20, illetve 25:
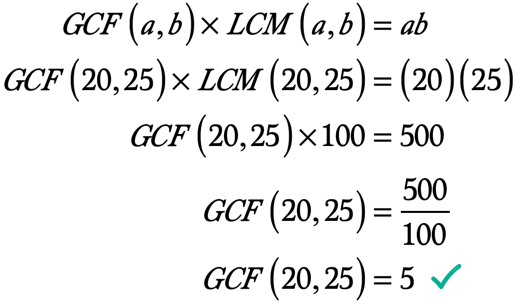
4. Példa: Megtalálni a LCM 63 84 által első kiszámítása a GCF 63 84.
Ez a probléma nagyon hasonlít a #3 példához. Az egyetlen különbség az, hogy először kiszámítja a GCF-et az LCM helyett, a probléma utasításai szerint.,
találjuk meg a 63-as és a 84-es faktorokat. Használhatja a “rainbow method” technikát az adott egész számok faktorálására.
vegye figyelembe, hogy a két lista között a legnagyobb vagy legmagasabb közös tényező a 21.
63: 1, 3, 7, 9, 21, 63
84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
ezért a legnagyobb közös tényező a 63 és 84 a 21. Így GCF \ bal ({63,84} \ jobb) = 21.,
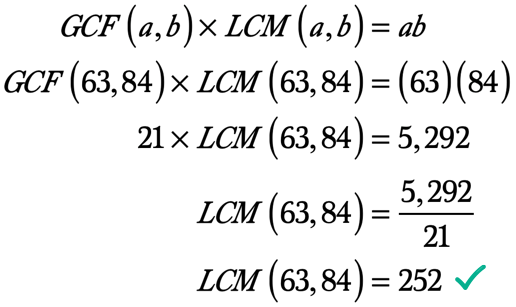
5.példa: keresse meg a 72-es és 90-es LCM-et a GCF-LCM formula.
mint már tudjuk, a GCF-LCM képlet segítségével két egész szám LCM-jét találjuk a GCF értékével.,
felsorolva mind a 72, mind a 90 tényezőt, van:
72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
amikor összehasonlítjuk a tényezők listáját, látjuk, hogy a 18 Az a tényező, amely mindkettőre közös, de a legnagyobb vagy a legnagyobb értékű. Ez azt jelenti, hogy a 72-es és a 90-es GCF 18, azaz GCF \ bal ({72,90} \ jobb) = 18.
készen állunk az alábbi értékek helyettesítésére a képletben.,
ab ab = \ left ({72} \right)\left ({90} \right) = 6,480
❖ GCF\left ({72,90} \right) = 18
itt van a számítás, hogy megtaláljuk az LCM-t, mivel már ismerjük a két egész szám GCF-jét és a terméküket.